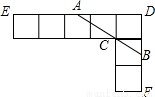
题目内容
 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.(1)若DA=
| 5 | 2 |
(2)若DA、DB是方程2x2-(2k+1)x-2=0的两根,求k的值;
(3)若A点在DE上移动,估计AB的长度的范围.
分析:(1)判断出△ACG∽△ABD,利用相似三角形的性质解答即可;
(2)直接根据根与系数的关系列出关于k的方程,解答即可;
(3)根据图形找出AB的最长和最短时点A的位置,继而求出对应的AB的长.
(2)直接根据根与系数的关系列出关于k的方程,解答即可;
(3)根据图形找出AB的最长和最短时点A的位置,继而求出对应的AB的长.
解答: 解:(1)如图,
解:(1)如图,
易得△ACG∽△ABD,
故
=
,
即
=
,
∴BD=
.
(2)根据根与系数的关系,DA+BD=
,
即
+
=
,
k=
.
(3)由题意知:当A点与E嗲重合时,AB的长度最大,
此时AB=
=
;
当A点在点H处时,AB的长度最小,
此时AB=
AD=2
.
故AB的长度范围为:2
≤AB≤
.
 解:(1)如图,
解:(1)如图,易得△ACG∽△ABD,
故
| AG |
| AD |
| CG |
| BD |
即
| 1.5 |
| 2.5 |
| 1 |
| BD |
∴BD=
| 5 |
| 3 |
(2)根据根与系数的关系,DA+BD=
| 2k+1 |
| 2 |
即
| 5 |
| 2 |
| 5 |
| 3 |
| 2k+1 |
| 2 |
k=
| 11 |
| 3 |
(3)由题意知:当A点与E嗲重合时,AB的长度最大,
此时AB=
| AD×AC |
| AG |
5
| ||
| 4 |
当A点在点H处时,AB的长度最小,
此时AB=
| 2 |
| 2 |
故AB的长度范围为:2
| 2 |
5
| ||
| 4 |
点评:此题考查了解直角三角形、相似三角形的性质、根与系数的关系等内容,结合图形的性质解答,事半功倍.

练习册系列答案
相关题目
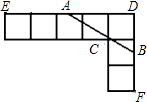
 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.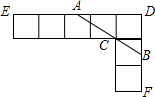 如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B.
如图,由七个边长为1的正方形组成,过C点作直线交DE于A,交DF于B. ,求DB的长;
,求DB的长; ,求DB的长;
,求DB的长;
 ,求DB的长;
,求DB的长;