Question

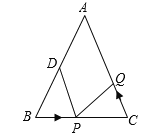
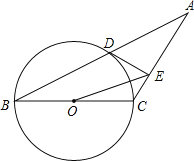
【题目】如图，已知等腰三角形ABC的底角为30°，以BC为直径的⊙O与底边AB交于点D，过D作DE⊥AC，垂足为E．

（1）证明：DE为⊙O的切线；

（2）连接OE，若BC=8，求△OEC的面积．

Answer 1

【答案】（1）证明见解析；（2）S△OEC=2.

【解析】试题（1）由△ABC 是等腰三角形，可得CA=CB，则∠A = ∠B，又由OD=OB，可得∠ODB = ∠B，所以∠A = ∠ODB，即OD ∥AC，又OD⊥DE， AC⊥DE，所以DE是⊙O的切线继而可证得结论；（2）连接DC．首先证△ODC为等边三角形，再根据三角函数的性质，求得AD、CD、ED、AE、EC的长，然后求得S△OEC =OCEF.

∵OB=OD,

∴∠OBD=∠ODB.

又∵∠A=∠B=30°

∴∠A=∠ODB,

∴DO∥AC

∵DE⊥AC

∴OD⊥DE．

∴DE为⊙O的切线．

（2）连接DC．

∵∠OBD=∠ODB=30°，

∴∠DOC=60°．

∴△ODC为等边三角形．

∴∠ODC=60°，

∴∠CDE=30°

又∵BC=8，

∴DC=4,

∴CE=2．

过点E作EF⊥BC，交BC的延长线于点F．

∵∠ECF=∠A+∠B=60°,

∴EF=CE·sin60°=2×=

∴S△OEC =OCEF=×4×=2.

故答案为：