题目内容
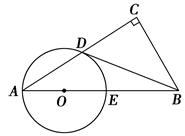
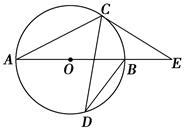
如图，AB是⊙O的直径，C、D是⊙O上两点，∠CDB＝20°，过点C作⊙O的切线交AB的延长线于点E，则∠E等于( )
A．40° B．50° C．60° D．70°
A．40° B．50° C．60° D．70°
B
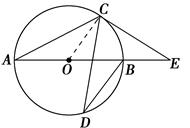
连接OC，如图所示：
∵圆心角∠BOC与圆周角∠CDB都对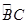
，
∴∠BOC＝2∠CDB，又∠CDB＝20°，
∴∠BOC＝40°，
又∵CE为圆O的切线，
∴OC⊥CE，即∠OCE＝90°，
则∠E＝90°－40°＝50°.
故选B.
∵圆心角∠BOC与圆周角∠CDB都对
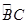，∴∠BOC＝2∠CDB，又∠CDB＝20°，
∴∠BOC＝40°，
又∵CE为圆O的切线，
∴OC⊥CE，即∠OCE＝90°，
则∠E＝90°－40°＝50°.
故选B.
练习册系列答案
相关题目
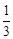圆周的一个扇形，将留下的扇形围成一个圆锥（接缝处不重叠），那么这个圆锥的高为 
