题目内容
如图,AB为⊙O的弦,AB=8,OC⊥AB于点D,交⊙O于点C,且CD=l,求⊙O的半径.


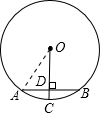
如图:
连接OA,由OC⊥AB于D,得:AD=DB=
AB=4.
设⊙O的半径为r,在Rt△OAD中,OA2=AD2+OD2
∴r2=(r-1)2+42
整理得:2r=17
∴r=
.
所以圆的半径是
.
连接OA,由OC⊥AB于D,得:AD=DB=
| 1 |
| 2 |
设⊙O的半径为r,在Rt△OAD中,OA2=AD2+OD2
∴r2=(r-1)2+42
整理得:2r=17
∴r=
| 17 |
| 2 |
所以圆的半径是
| 17 |
| 2 |


练习册系列答案
相关题目