题目内容
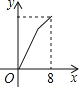
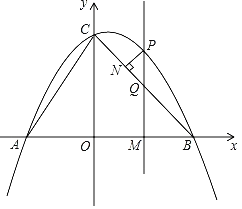
【题目】如图,抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,与y轴交于点C,连接AC,BC.点P是第一象限内抛物线上的一个动点,点P的横坐标为m.
(1)求此抛物线的表达式;
(2)过点P作PM⊥x轴,垂足为点M,PM交BC于点Q.试探究点P在运动过程中,是否存在这样的点Q,使得以A,C,Q为顶点的三角形是等腰三角形.若存在,请求出此时点Q的坐标,若不存在,请说明理由;
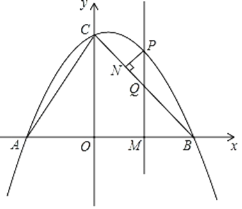
(3)过点P作PN⊥BC,垂足为点N.请用含m的代数式表示线段PN的长,并求出当m为何值时PN有最大值,最大值是多少?
【答案】(1)![]() (2)存在,点Q的坐标为:Q(1,3)或(
(2)存在,点Q的坐标为:Q(1,3)或(![]() ,
,![]() );(3)PN=﹣
);(3)PN=﹣![]() (m﹣2)2+
(m﹣2)2+![]() ,当m=2时,PN的最大值为
,当m=2时,PN的最大值为![]() .
.
【解析】
(1)由二次函数交点式表达式,即可求解;
(2)分AC=AQ、AC=CQ、CQ=AQ三种情况,利用方程或方程组求解即可得到答案;
(3)利用等腰直角三角形的性质得到:PN=PQsin∠PQN=![]() 即可求解.
即可求解.
解:(1)![]() 抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,
抛物线y=ax2+bx+4交x轴于A(﹣3,0),B(4,0)两点,
设![]()
即:﹣12a=4,解得:![]()
则抛物线的表达式为![]()
(2)存在,理由:
![]()
![]()
![]() 点A、B、C的坐标分别为(﹣3,0)、(4,0)、(0,4),
点A、B、C的坐标分别为(﹣3,0)、(4,0)、(0,4),
则AC=5,AB=7,BC=![]() ,∠OBC=∠OCB=45°,
,∠OBC=∠OCB=45°,
将点B、C的坐标代入一次函数表达式:y=kx+b并解得:y=﹣x+4…①,
同理可得直线AC的表达式为:![]() ,
,
①当AC=AQ时,如图1,
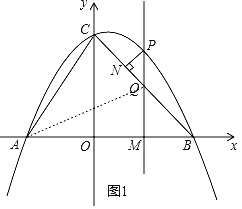
则AC=AQ=5,
设:QM=MB=n,则AM=7﹣n,
由勾股定理得:![]()
解得:n=3或4(舍去4),
故点Q(1,3);
②当AC=CQ时,如图1,
CQ=5,则BQ=BC﹣CQ=![]()
则QM=MB=![]() ,
,
故点Q(![]() ,
,![]() );
);
③当CQ=AQ时,则![]() 在
在![]() 的垂直平分线上,
的垂直平分线上,
设直线AC的中点为K(![]() ,2),
,2),
过点![]() 与CA垂直直线的表达式中的k值为
与CA垂直直线的表达式中的k值为![]() ,
,
直线![]() 的表达式为:
的表达式为:![]() ②,
②,
联立①②并解得:![]() (舍去);
(舍去);
故点Q的坐标为:Q(1,3)或(![]() ,
,![]() );
);
(3)设点![]() ,则点Q(m,﹣m+4),
,则点Q(m,﹣m+4),
∵OB=OC,∴∠ABC=∠OCB=45°=∠PQN,
PN=PQsin∠PQN=![]()
∵![]()
∴PN有最大值,
当m=2时,PN的最大值为:![]() .
.

 备战中考寒假系列答案
备战中考寒假系列答案【题目】某公司为了到高校招聘大学生,为此设置了三项测试:笔试、面试、实习.学生的最终成绩由笔试面试、实习依次按3:2:5的比例确定.公司初选了若干名大学生参加笔试,面试,并对他们的两项成绩分别进行了整理和分析.下面给出了部分信息:
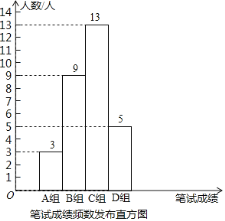
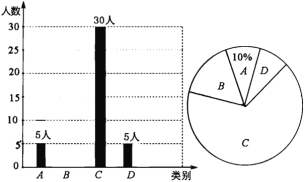
①公司将笔试成绩(百分制)分成了四组,分别为A组:60≤x<70,B组:70≤x<80,C组:80≤x<90,D组:90≤x<100;并绘制了如下的笔试成绩频数分布直方图.其中,C组的分数由低到高依次为:80,81,82,83,83,84,84,85,86,88,88,88,89.
②这些大学生的笔试、面试成绩的平均数、中位数、众数、最高分如下表:
平均数 | 中位数 | 众数 | 最高分 | |
笔试成绩 | 81 | m | 92 | 97 |
面试成绩 | 80.5 | 84 | 86 | 92 |
根据以上信息,回答下列问题:
(1)这批大学生中笔试成绩不低于88分的人数所占百分比为 .
(2)m= 分,若甲同学参加了本次招聘,他的笔试、面试成绩都是83分,那么该同学成绩排名靠前的是 成绩,理由是 .
(3)乙同学也参加了本次招聘,笔试成绩虽不是最高分,但也不错,分数在D组;面试成绩为88分,实习成绩为80分由表格中的统计数据可知乙同学的笔试成绩为 分;若该公司最终录用的最低分数线为86分,请通过计算说明,该同学最终能否被录用?