题目内容
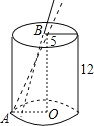
【题目】如图是一个圆柱形饮料罐,底面半径为5cm,高为12cm,上底面中心有一个小圆孔,一条长为20cm可到达底部的直吸管在罐外部分a长度(罐壁厚度和小圆孔大小忽略不计)范围是( )

A.8≤a≤15 B.5≤a≤8 C.7≤a≤8 D.7≤a≤15
【答案】C
【解析】
试题分析:如图,当吸管底部在O点时吸管在罐内部分最短,此时罐内部分就是圆柱形的高;当吸管底部在A点时吸管在罐内部分最长,此时可以利用勾股定理在Rt△ABO中求出,然后可得罐外部分a长度范围.
解:如图,当吸管底部在O点时吸管在罐内部分最短,
此时罐内部分就是圆柱形的高,
罐外部分a=20﹣12=8(cm);
当吸管底部在A点时吸管在罐内部分最长,
即线段AB的长,
在Rt△ABO中,
AB=![]() =
=![]() =13(cm),
=13(cm),
罐外部分a=20﹣13=7(cm),
所以7≤a≤8.
故选:C.

练习册系列答案
相关题目