题目内容
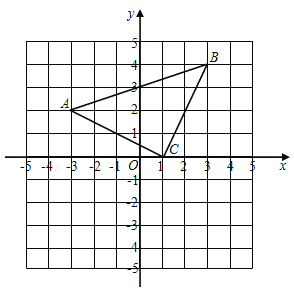
【题目】如图,已知直线AB与![]() 轴交于点C,与双曲线
轴交于点C,与双曲线![]() 交于A(3,
交于A(3,![]() )、B(-5,
)、B(-5,![]() )两点.AD⊥
)两点.AD⊥![]() 轴于点D,BE∥
轴于点D,BE∥![]() 轴且与
轴且与![]() 轴交于点E.
轴交于点E.
(1)求点B的坐标及直线AB的解析式;
(2)判断四边形CBED的形状,并说明理由.

【答案】(1)点B的坐标是(-5,-4);直线AB的解析式为:![]()
(2)四边形CBED是菱形.理由见解析
【解析】
(1)根据反比例函数图象上点的坐标特征,将点A代入双曲线方程求得k值,即利用待定系数法求得双曲线方程;然后将B点代入其中,从而求得a值;设直线AB的解析式为y=mx+n,将A、B两点的坐标代入,利用待定系数法解答;
(2)由点C、D的坐标、已知条件“BE∥x轴”及两点间的距离公式求得,CD=5,BE=5,且BE∥CD,从而可以证明四边形CBED是平行四边形;然后在Rt△OED中根据勾股定理求得ED=5,所以ED=CD,从而证明四边形CBED是菱形.
解:(1)∵双曲线![]() 过A(3,
过A(3,![]() ),∴
),∴![]() .把B(-5,
.把B(-5,![]() )代入
)代入![]() ,
,
得![]() . ∴点B的坐标是(-5,-4)
. ∴点B的坐标是(-5,-4)
设直线AB的解析式为![]() ,
,
将 A(3,![]() )、B(-5,-4)代入得,
)、B(-5,-4)代入得,
 , 解得:
, 解得:![]() .
.
∴直线AB的解析式为:![]()
(2)四边形CBED是菱形.理由如下:
点D的坐标是(3,0),点C的坐标是(-2,0).
∵ BE∥![]() 轴, ∴点E的坐标是(0,-4).
轴, ∴点E的坐标是(0,-4).
而CD =5, BE=5,且BE∥CD.
∴四边形CBED是平行四边形
在Rt△OED中,ED2=OE2+OD2,∴ ED=![]() =5,∴ED=CD.
=5,∴ED=CD.
∴□CBED是菱形

 阅读快车系列答案
阅读快车系列答案【题目】二次函数y=ax2+bx+c(a,b,c 为常数,且a≠0)的图像上部分点的横坐标x和纵
坐标y的对应值如下表
x | … | -1 | 0 | 1 | 2 | 3 | … |
y | … | -3 | -3 | -1 | 3 | 9 | … |
关于x的方程ax2+bx+c=0一个负数解x1满足k<x1<k+1(k为整数),则k=________.