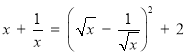��Ŀ����
����Ŀ��ij��ij��ѧ��֯����ѧ��ȥij�ؿ�չ��ѧ���л���ڲμӴ˴λ��ʦ���У���ÿλ��ʦ��17��ѧ������ʣ12��ѧ��û�˴�����ÿλ��ʦ��18��ѧ��������һλ��ʦ�ٴ�4��ѧ�������мס������ִ�ͳ������ǵ��ؿ�������������ʾ��
���ֿͳ� | ���ֿͳ� | |
�ؿ���/����/���� | 30 | 42 |
���/��Ԫ/���� | 300 | 400 |
ѧУ�ƻ��˴���ѧ���л����ܷ��ò�����3100Ԫ��Ϊ�˰�ȫ��ÿ���ͳ�������Ҫ��2����ʦ��
��1���μӴ˴���ѧ���л����ʦ��ѧ�����ж����ˣ�
��2���ټ�Ҫ��֤����ʦ�����г�������Ҫ��֤ÿ���ͳ�������Ҫ��2����ʦ�������ü����ͳ���
��������õ���Сֵ��
���𰸡���1����ʦ��16����ѧ����284������2��������8���ͳ�������������Ϊ2900Ԫ��
��������
��1�������ʦ��x����ѧ����y�����ó���Ԫһ�η����飬������ɣ���2���ٸ��������������ܳ���![]() ��ȡ��Ϊ8�����������������������x�����ֿͳ�������ֿͳ���Ϊ����8-x������������ó�400x+300��8-x����3100���ó�xȡֵ��Χ�������ó�����.
��ȡ��Ϊ8�����������������������x�����ֿͳ�������ֿͳ���Ϊ����8-x������������ó�400x+300��8-x����3100���ó�xȡֵ��Χ�������ó�����.
�⣺��1������ʦ��x����ѧ����y���������⣬�з�����Ϊ![]() ����ã�
����ã�![]() ��
��
����ʦ��16����ѧ����284����
��2���١�ÿ���ͳ�������Ҫ��2����ʦ���������������ܴ���8����Ҫ��֤300��ʦ���г�����������������С��![]() ��ȡ��Ϊ8������
��ȡ��Ϊ8������
������8���ͳ���
��������x�����ֿͳ�������ֿͳ���Ϊ��8��x������
�߳��ܷ��ò�����3100Ԫ��
��400x+300��8��x����3100����ã�x��7��
Ϊʹ300��ʦ������������42x+30��8��x����300����ã�x��5��
��5��x��7��x��������
�����ֳ������ߣ����������ֳ������٣��������ͣ�
�����ü��ֿͳ�3�������ֿͳ�5������������Ϊ2900Ԫ��

 �����Ļ���������人������ϵ�д�
�����Ļ���������人������ϵ�д� ���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д�
���������ּ���ÿһ��ȫ�º�����ҵ��ϵ�д� ��ٽ������½������������ϵ�д�
��ٽ������½������������ϵ�д�����Ŀ��ɽ�����г�Խ��Խ�ܵ���ѧ����ϲ��������Ʒ�����Ͷ���г���ij���о�Ӫ��A�ͳ�1�·������ܶ�Ϊ50000Ԫ��2�·������ܶ��1�·ݼ���20%��ÿ�����ۼ۱�1�·ݽ���400Ԫ������������������������ͬ��
��1����2�·�A�ͳ�ÿ���ۼ۶���Ԫ��
��2���ó��мƻ��½�һ��A�ͳ����¿�B�ͳ���60������B�ͳ��Ľ�������������A�ͳ���������������������������õ���������Ƕ���Ԫ��
A��B�����ͺų�����Ľ��������ۼ۸����
A�ͳ� | B�ͳ� | |
�����۸�Ԫ�� | 1100 | 1400 |
���ۼ۸�Ԫ�� | 2�·ݵ����ۼ۸� | 2000 |
����Ŀ���ס�������ͬѧ�ֱ����6�����ѵ����ѵ���ɼ�����λ���������±�
��һ�� | �ڶ��� | ������ | ���Ĵ� | ����� | ������ | |
�� | 9 | 8 | 6 | 7 | 8 | 10 |
�� | 8 | 7 | 9 | 7 | 8 | 8 |
�����ǵ�ѵ���ɼ������·���������˵����ȷ���ǣ�������
A. ����ѵ���ɼ���ƽ������ͬ B. ����ѵ���ɼ�����λ����ͬ
C. ����ѵ���ɼ���������ͬ D. ����ѵ���ɼ��ķ��ͬ