题目内容
 一轮船正向东以30海里/小时的速度航行,在A点处发现北偏东60°的方向有一小岛C,又航行2小时后,发现小岛C在北偏东30°方向,为了确定小岛C的具体位置,现在以A点为坐标原点,以正北方向为y轴正方向,以正东方向为x轴正方向建立平面直角坐标系(如图所示).请你帮助计算小岛所在位置的坐标(在直角三角形中,30°角所对的直角边为斜边的一半).
一轮船正向东以30海里/小时的速度航行,在A点处发现北偏东60°的方向有一小岛C,又航行2小时后,发现小岛C在北偏东30°方向,为了确定小岛C的具体位置,现在以A点为坐标原点,以正北方向为y轴正方向,以正东方向为x轴正方向建立平面直角坐标系(如图所示).请你帮助计算小岛所在位置的坐标(在直角三角形中,30°角所对的直角边为斜边的一半).分析:过点C作BC⊥x轴于B,根据已知可求得点AB和BC的长,从而根据已知求C的坐标.
解答:解:过点C作BC⊥x轴于B, 过D作DE⊥AB,
过D作DE⊥AB,
由已知可知:∠1=∠2=30°,
∴∠CDB=60°,∠ACD=∠DCB=30°,
∴CD=AD=2×30=60海里,
在Rt△CDB中,∠DCB=30°,
∴DB=
CD=30海里,
∴BC=30
海里,AB=90海里,
∴C点的坐标为(90,30
).
 过D作DE⊥AB,
过D作DE⊥AB,由已知可知:∠1=∠2=30°,
∴∠CDB=60°,∠ACD=∠DCB=30°,
∴CD=AD=2×30=60海里,
在Rt△CDB中,∠DCB=30°,
∴DB=
| 1 |
| 2 |
∴BC=30
| 3 |
∴C点的坐标为(90,30
| 3 |
点评:本题主要考查了方向角含义,直角三角形中,30°角所对的直角边为斜边的一半,正确记忆三角函数的定义是解决本题的关键.

练习册系列答案
相关题目
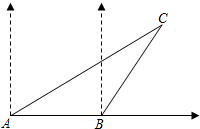 如图,一艘渔船正以30海里/小时的速度由西向东赶鱼群,在A处看风小岛C在船的北偏东60度.40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30度.已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向东追赶鱼群,是否有进入危险区的可能?
如图,一艘渔船正以30海里/小时的速度由西向东赶鱼群,在A处看风小岛C在船的北偏东60度.40分钟后,渔船行至B处,此时看见小岛C在船的北偏东30度.已知以小岛C为中心周围10海里以内为我军导弹部队军事演习的着弹危险区,问这艘渔船继续向东追赶鱼群,是否有进入危险区的可能?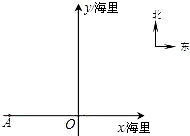 分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上.
分钟后,渔船行至O处,此时看见小岛B在船的北偏东30°.在如图所示的坐标系中,点O为坐标原点,点A位于x轴上. (2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.
(2013•湘西州)钓鱼岛自古以来就是中国的神圣领土,为宣誓主权,我海监船编队奉命在钓鱼岛附近海域进行维权活动,如图,一艘海监船以30海里/小时的速度向正北方向航行,海监船在A处时,测得钓鱼岛C在该船的北偏东30°方向上,航行半小时后,该船到达点B处,发现此时钓鱼岛C与该船距离最短.