Question

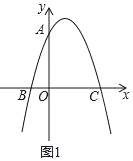
【题目】已知，如图1，抛物线y=ax2+bx+3与x轴交于点B、C，与y轴交于点A，且AO=CO，BC=4．

（1）求抛物线解析式；

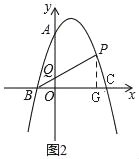
（2）如图2，点P是抛物线第一象限上一点，连接PB交y轴于点Q，设点P的横坐标为t，线段OQ长为d，求d与t之间的函数关系式；

（3）在（2）的条件下，过点Q作直线l⊥y轴，在l上取一点M（点M在第二象限），连接AM，使AM=PQ，连接CP并延长CP交y轴于点K，过点P作PN⊥l于点N，连接KN、CN、CM．若∠MCN+∠NKQ=45°时，求t值．

Answer 1

【答案】（1）y=﹣x2+2x+3（2）d=﹣t+3（0＜t＜3）（3）

【解析】试题分析：（1）先令x=0代入抛物线的解析式中求得与y轴交点A的坐标，根据OA=OC可得C的坐标，从而得B的坐标，利用待定系数法求抛物线解析式；

（2）如图2，设P（t，-t2+2t+3）（0<t<3），证明△BOQ∽△BGP，列比例式可得结论；

（3）如图3，作辅助线，构建全等三角形和等腰直角三角形，先得QN=OG=AQ=t，则△AQN是等腰直角三角形，得AN=t，由PG∥OK，得,，求得AK=3t，证明△NGC是等腰直角三角形，及△AKN∽△NMC，则，代入可得t的值，并根据（2）中的点P只在第一象限进行取舍．

解：（1）如图1，当x=0时，y=3，

∴A（0，3），

∴OA=OC=3，

∵BC=4，

∴OB=1，

∴B（﹣1，0），C（3，0），

把B（﹣1，0），C（3，0）代入抛物线y=ax2+bx+3中得：，

解得：，

∴抛物线的解析式为：y=﹣x2+2x+3；

（2）如图2，设P（t，﹣t2+2t+3）（0＜t＜3），

过P作PG⊥x轴于G，

∵OQ∥PG，

∴△BOQ∽△BGP，

∴，

∴，

∴d==﹣t+3（0＜t＜3）；

（3）如图3，连接AN，延长PN交x轴于G，

由（2）知：OQ=3﹣t，OA=3，

∴AQ=OA﹣OQ=3﹣（3﹣t）=t，

∴QN=OG=AQ=t，

∴△AQN是等腰直角三角形，

∴∠QAN=45°，AN=t，

∵PG∥OK，

∴，

∴，

OK=3t+3，

AK=3t，

∵∠QAN=∠NKQ+∠ANK，

∴∠NKQ+∠ANK=45°，

∵∠MCN+∠NKQ=45°，

∴∠ANK=∠MCN，

∵NG=CG=3﹣t，

∴△NGC是等腰直角三角形，

∴NC=（3﹣t），∠GNC=45°，

∴∠CNH=∠NCM+∠NMC=45°，

∴∠NKQ=∠NMC，

∴△AKN∽△NMC，

∴，

∵AQ=QN=t，AM=PQ，

∴Rt△AQM≌△Rt△QNP（HL），

∴MQ=PN=﹣t2+2t+3﹣（3﹣t）=﹣t2+3t，

∴，

t2﹣7t+9=0，

t1=＞3，t2=，

∵0＜t＜3，

∴t1＞3，不符合题意，舍去，

∴t=．