ΧβΡΩΡΎ»ί
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ≥ΛΖΫ–Έ![]() ÷–Θ§
÷–Θ§![]() cmΘ§
cmΘ§![]() cmΘ§Βψ
cmΘ§Βψ![]() ΈΣ
ΈΣ![]() ΒΡ÷–Βψ.»τΒψ
ΒΡ÷–Βψ.»τΒψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ“‘1 cm/sΒΡΥΌΕ»”…Βψ
…œ“‘1 cm/sΒΡΥΌΕ»”…Βψ![]() œρΒψ
œρΒψ![]() ‘ΥΕ·Θ§ΒΫΒψ
‘ΥΕ·Θ§ΒΫΒψ![]() ±≤ΜΕ·.Ά§ ±Θ§Βψ
±≤ΜΕ·.Ά§ ±Θ§Βψ![]() ‘ΎœΏΕΈ
‘ΎœΏΕΈ![]() …œ”…Βψ
…œ”…Βψ![]() œρΒψ
œρΒψ![]() ‘ΥΕ·.
‘ΥΕ·.
(1)»τΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ
ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§Ψ≠Ιΐ1 sΚσΘ§
ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§Ψ≠Ιΐ1 sΚσΘ§![]() ”κ
”κ![]() «Ζώ»ΪΒ»?«κΥΒΟςάμ”…Θ§≤Δ≈–Εœ¥Υ ±œΏΕΈ
«Ζώ»ΪΒ»?«κΥΒΟςάμ”…Θ§≤Δ≈–Εœ¥Υ ±œΏΕΈ![]() ΚΆ
ΚΆ![]() ΒΡΈΜ÷ΟΙΊœΒ;
ΒΡΈΜ÷ΟΙΊœΒ;
(2)»τΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ
ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§‘ΥΕ· ±ΦδΈΣ
ΒΡ‘ΥΕ·ΥΌΕ»œύΒ»Θ§‘ΥΕ· ±ΦδΈΣ![]() sΘ§…η
sΘ§…η![]() ΒΡΟφΜΐΈΣ
ΒΡΟφΜΐΈΣ![]() cm2Θ§«κ”ΟΚ§
cm2Θ§«κ”ΟΚ§![]() ΒΡ¥ζ ΐ Ϋ±μ Ψ
ΒΡ¥ζ ΐ Ϋ±μ Ψ
(3)»τΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ
ΒΡ‘ΥΕ·ΥΌΕ»”κΒψ![]() ΒΡ‘ΥΕ·ΥΌΕ»≤ΜœύΒ»Θ§Β±Βψ
ΒΡ‘ΥΕ·ΥΌΕ»≤ΜœύΒ»Θ§Β±Βψ![]() ΒΡ‘ΥΕ·ΥΌΕ»ΈΣΕύ…Ό ±Θ§ΡήΙΜ Ι
ΒΡ‘ΥΕ·ΥΌΕ»ΈΣΕύ…Ό ±Θ§ΡήΙΜ Ι![]() ”κ
”κ![]() »ΪΒ»?
»ΪΒ»?
ΓΨ¥πΑΗΓΩΘ®1Θ©ΦϊΫβΈωΘΜΘ®2Θ©S=![]()
![]() t+6;Θ®3Θ©
t+6;Θ®3Θ©![]() cm/s
cm/s
ΓΨΫβΈωΓΩ
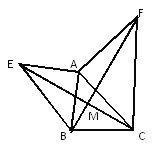
Θ®1Θ©±ΨΧβΚή»ί“Ή÷ΛΟςΓςAEPΓ’ΓςBPQΘ§’β―υΩ…ΒΟ≥ωΓœAEP=ΓœBPQΘ§“ρΈΣΓœAEP+ΓœAPE=90ΓψΘ§Ω…ΒΟ≥ωΓœBPQ+ΓœAPE=90ΓψΘ§’βΦ¥Ω…≈–Εœ≥ωΫα¬έΘ°
Θ®2Θ©Ω…Ζ÷±π”Οt±μ Ψ≥ωAPΓΔBQΓΔBPΓΔCQΒΡ≥ΛΕ»Θ§»ΜΚσ”ΟΨΊ–ΈΒΡΟφΜΐΦθ»ΞΓςAPEΓΔΓςBPQΦΑΧί–ΈEDCQΒΡΟφΜΐΦ¥Ω…ΒΟ≥ωΓςPEQΒΡΟφΜΐΈΣScm2Θ°
Θ®3Θ©…ηQ‘ΥΕ·ΒΡΥΌΕ»ΈΣxcm/sΘ§‘ρΗυΨίΓςAEP”κΓςBQPΒΟ≥ωAP=BPΓΔAE=BQΜρAP=BQΘ§AE=BPΘ§¥”ΕχΩ…Ν–≥ωΖΫ≥ΧΉιΘ§Ϋβ≥ωΦ¥Ω…ΒΟ≥ω¥πΑΗΘ°
(1)ΓΏ≥ΛΖΫ–ΈABCD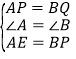 Θ§
Θ§
ΓύΓœA=ΓœB=90ΓψΘ§
ΓΏΒψEΈΣADΒΡ÷–ΒψΘ§AD=6cmΘ§
ΓύAE=3cmΘ§
”÷ΓΏPΚΆQΒΡΥΌΕ»œύΒ»Ω…ΒΟ≥ωAP=BQ=1cmΘ§BP=3Θ§
ΓύAE=BPΘ§
‘ΎΓςAEPΚΆΓςBQP÷–Θ§
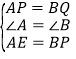 Θ§
Θ§
ΓύΓςAEPΓ’ΓςBPQΘ§
ΓύΓœAEP=ΓœBPQΘ§
”÷ΓΏΓœAEP+ΓœAPE=90ΓψΘ§
Ι Ω…ΒΟ≥ωΓœBPQ+ΓœAPE=90Γψ,Φ¥ΓœEPQ=90ΓψΘ§
Φ¥EPΓΆPQ.
(2)Ν§Ϋ”QE,”…Χβ“βΒΟΘΚAP=BQ=t,BP=4t,CQ=6t,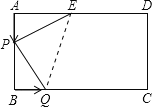
SPEQ=SABCDSBPQSEDCQSAPE=ADΓΝAB![]() AEΓΝAP
AEΓΝAP![]() BPΓΝBQ
BPΓΝBQ![]() (DE+CQ)ΓΝCD=24
(DE+CQ)ΓΝCD=24![]() ΓΝ3t
ΓΝ3t![]() t(4t)
t(4t) ![]() ΓΝ4(3+6t)=
ΓΝ4(3+6t)= ![]()
![]() t+6Θ§
t+6Θ§
(3)…ηΒψQΒΡ‘ΥΕ·ΥΌΕ»ΈΣxcm/sΘ§
ΔΌΨ≠ΙΐyΟκΚσ,ΓςAEPΓ’ΓςBQPΘ§‘ρAP=BPΘ§AE=BQΘ§
Γύ![]() Θ§
Θ§
ΫβΒΟΘΚ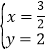 Θ§
Θ§
Φ¥ΒψQΒΡ‘ΥΕ·ΥΌΕ»ΈΣ![]() cm/s ±Ρή ΙΝΫ»ΐΫ«–Έ»ΪΒ».
cm/s ±Ρή ΙΝΫ»ΐΫ«–Έ»ΪΒ».![]()
ΔΎΨ≠ΙΐyΟκΚσ,ΓςAEPΓ’ΓςBPQΘ§‘ρAP=BQΘ§AE=BPΘ§
Γύy=xy,3=4yΘ§
ΫβΒΟΘΚ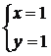 (…α»Ξ).
(…α»Ξ).
Ήέ…œΥυ ω,ΒψQΒΡ‘ΥΕ·ΥΌΕ»ΈΣ![]() cm/s ±Ρή ΙΝΫ»ΐΫ«–Έ»ΪΒ»ΓΘ
cm/s ±Ρή ΙΝΫ»ΐΫ«–Έ»ΪΒ»ΓΘ

 ≥θ÷–―ß“ΒΩΦ ‘ΒΦ”κΝΖœΒΝ–¥πΑΗ
≥θ÷–―ß“ΒΩΦ ‘ΒΦ”κΝΖœΒΝ–¥πΑΗ