题目内容
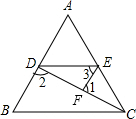 如图,已知∠1+∠2=180°,∠3=∠B.
如图,已知∠1+∠2=180°,∠3=∠B.
(1)试判断∠AED与∠ACB的大小关系,并说明你的理由.
(2)若D、E、F分别是AB、AC、CD边上的中点,S四边形ADFE=4(平方单位),求S△ABC.
 解:(1)相等.
解:(1)相等.∵∠1+∠2=180°,∠1+∠DFE=180
∴∠2=∠DFE
又∵∠3=∠B
∴△BCD∽△EDF,∠EDF=∠BCD
∴DE∥BC,∠AED=∠ACB;
(2)过C作CG⊥AB于G交EF于H
∵EF是△ACD的中位线
∴GH=CH=
 CG,EF=
CG,EF= AD
AD又∵四边形ADFE是梯形
∴S四边形ADFE=
 (AD+EF)×GH=
(AD+EF)×GH= ×
× AD×
AD× CG=
CG= AD•CG=4
AD•CG=4∴AD•CG=
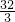
∴S△ABC=
 AB•CG=
AB•CG= ×2AD•CG=AD•CG
×2AD•CG=AD•CG∴S△ABC=
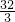 .
.分析:(1)根据角相等可得出三角相似,进而求出DE∥BC,∠AED=∠ACB;
(2)根据D、E、F分别是AB、AC、CD边上的中点可求出四边形ADFE是梯形,作出三角形的高线即可求出梯形与三角形面积的关系.
点评:此题考查的是三角形的中位线定理及梯形的面积公式,比较简单.

练习册系列答案
相关题目
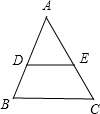 如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )
如图,已知:DE∥BC,AB=14,AC=18,AE=10,则AD的长为( )A、
| ||
B、
| ||
C、
| ||
D、
|
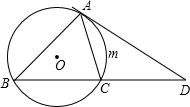 =2,∠ADC=30°
=2,∠ADC=30°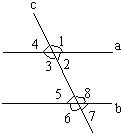 30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
30、如图,已知直线a,b与直线c相交,下列条件中不能判定直线a与直线b平行的是( )
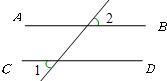 13、如图,已知直线AB∥CD,∠1=50°,则∠2=
13、如图,已知直线AB∥CD,∠1=50°,则∠2=