Question

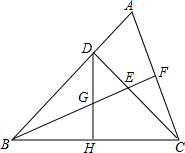已知：如图，在△ABC中，CD⊥AB，CD=BD，BF平分∠DBC，与CD，AC分别交于点E、点F，且DA=DE，H是BC边的中点，连结DH与BE相交于点G．
（1）求证：△EBD≌△ACD；
（2）求证：点G在∠DCB的平分线上；
（3）试探索CF、GF和BG之间的等量关系，并证明你的结论．

Answer 1

分析：（1）由全等三角形的判定定理SAS证得结论；
（2）如图，过点G作GM⊥AB，GN⊥DC．欲证明点G在∠DCB的平分线上，只需证得GH=GN；
（3）BG²=GF²+CF²．连接GC．由（1）中的全等三角形的性质得到∠1=∠2．则易证∠BFC=90°，所以根据勾股定理得到CG²=GF²+CF²．由“DH是BC的垂直平分线”得到
BG=CG，所以BG²=GF²+CF²．

解答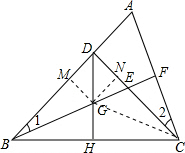：（1）证明：∵CD⊥AB，
∴∠BDE=∠CDA=90°．
在△EBD与△ACD中，

DE=DA ∠BDE=∠CDA BD=CD

，
∴△CBD≌△ACD（SAS）；

（2）证明：如图，过点G作GM⊥AB，GN⊥DC．
∵BD=CD，H是BC中点，
∴DH平分∠BDC，DH⊥BC．
∵GM⊥AB，GN⊥DC
∴GM=GN
∵BF平分∠ABC，GM⊥AB，GH⊥BC，
∴GM=GH，
∴GH=GN，
∴点G在∠DCB的平分线上；

（3）解：BG²=GF²+CF²．
理由如下：连接GC．由（1）知，△CBD≌△ACD，则∠1=∠2．
∵∠2+∠A=90°，
∴∠1+∠A=90°，
∴∠BFC=90°
∴CG²=GF²+CF²．
∵DH是BC的垂直平分线
∴BG=CG，
∴BG²=GF²+CF²．

点评：本题综合考查了全等三角形的判定与性、勾股定理以及角平分线的性质．全等三角形的判定是结合全等三角形的性质证明线段和角相等的重要工具．在判定三角形全等时，关键是选择恰当的判定条件．