题目内容
【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF;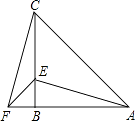
(1)求证:Rt△ABE≌Rt△CBF;
(2)求证:AB=CE+BF;
(3)若∠CAE=30°,求∠ACF度数.
【答案】
(1)证明:∵∠ABC=90°,
∴∠ABE=∠CBF=90°,
在Rt△ABE和Rt△CBF中,
![]() ,
,
∴Rt△ABE≌Rt△CBF(HL)
(2)证明:∵Rt△ABE≌Rt△CBF,
∴AB=BC,BE=BF,
∵BC=BE+CE,
∴AB=CE+BF
(3)∵AB=CB,∠ABC=90°,∠CAE=30°,∠CAB=∠CAE+∠EAB,
∴∠BCA=∠BAC=45°,
∴∠EAB=15°,
∵Rt△ABE≌Rt△CBF,
∴∠EAB=∠FCB,
∴∠FCB=15°,
∴∠ACF=∠FCB+∠BCA=15°+45°=60°,
即∠ACF=60°
【解析】(1)易由由所给条件已有“HL”得到Rt△ABE≌Rt△CBF。
(2)由(1)得Rt△ABE≌Rt△CBF,可由等量代换得到AB=CE+BF;
(3)由等腰直角三角形性质易得∠BCA=∠BAC=45°题干给了∠CAE=30°,所以易得∠EAB=15°,由(1)中相似可知∠FCB=15°即∠ACF=60°

练习册系列答案
相关题目