题目内容
【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE. 探究: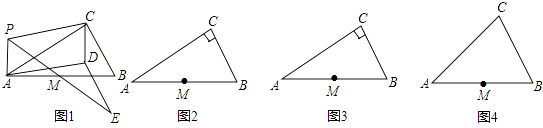
(1)请猜想与线段DE有关的三个结论;
(2)请你利用图2,图3选择不同位置的点P按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明; 如果你认为你写的结论是错误的,请用图2或图3加以说明;
(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE有关的结论(直接写答案).
【答案】
(1)解:DE∥BC,DE=BC,DE⊥AC
(2)解:如图4,如图5.

(3)解:方法一:
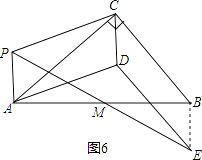
如图6,
连接BE,
∵PM=ME,AM=MB,∠PMA=∠EMB,
∴△PMA≌△EMB.
∵PA=BE,∠MPA=∠MEB,
∴PA∥BE.
∵平行四边形PADC,
∴PA∥DC,PA=DC.
∴BE∥DC,BE=DC,
∴四边形DEBC是平行四边形.
∴DE∥BC,DE=BC.
∵∠ACB=90°,
∴BC⊥AC,
∴DE⊥AC.
方法二:
如图7,连接BE,PB,AE,
∵PM=ME,AM=MB,
∴四边形PAEB是平行四边形.
∴PA∥BE,PA=BE,
余下部分同方法一:

方法三:
如图8,连接PD,交AC于N,连接MN,
∵平行四边形PADC,
∴AN=NC,PN=ND.
∵AM=BM,AN=NC,
∴MN∥BC,MN= ![]() BC.
BC.
又∵PN=ND,PM=ME,
∴MN∥DE,MN= ![]() DE.
DE.
∴DE∥BC,DE=BC.
∵∠ACB=90°,
∴BC⊥AC.
∴DE⊥AC.

(4)解:如图9,DE∥BC,DE=BC.

【解析】连接BE,根据边角边可证△PAM和△EBM全等,可得EB和PA既平行又相等,而PA和CD既平行且相等,所以DE和BC平行相等,又因为BC⊥AC,所以DE也和AC垂直.以下几种情况虽然图象有所变化,但是证明方法一致.
【考点精析】本题主要考查了平行四边形的性质的相关知识点,需要掌握平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】为建设秀美龙江,某学校组织师生参加一年一度的植树绿化工作,准备租用7辆客车,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车x辆,租车总费用为y元,
甲种客车 | 乙种客车 | |
载客量/(人/辆) | 60 | 40 |
租金/(元/辆) | 360 | 300 |
(1)求出y(单位:元)与x(单位:辆)之间的函数关系式。
(2)若该校共有350名师生前往参加劳动,共有多少种租车方案?
(3)带队老师从学校预支租车费用2400元,试问预支的租车费用是否可有结余?若有结余,最多可结余多少元。
【题目】6月5日是世界环境日,为了普及环保知识,增强环保意识,某市第一中学举行了“环保知识竞赛”,参赛人数1000人,为了了解本次竞赛的成绩情况,学校团委从中抽取部分学生的成绩(满分为100分,得分取整数)进行统计,并绘制出不完整的频率分布表和不完整的频数分布直方图如下:

(1)直接写出a的值,并补全频数分布直方图.
分组 | 频数 | 频率 |
49.5~59.5 | 0.08 | |
59.5~69.5 | 0.12 | |
69.5~79.5 | 20 | |
79.5~89.5 | 32 | |
89.5~100.5 | a |
(2)若成绩在80分以上(含80分)为优秀,求这次参赛的学生中成绩为优秀的约为多少人?
(3)若这组被抽查的学生成绩的中位数是80分,请直接写出被抽查的学生中得分为80分的至少有多少人?