题目内容
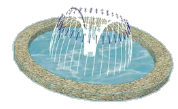
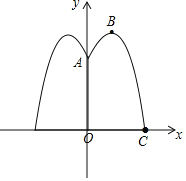
【题目】如图，公园中一正方形水池中有一喷泉，喷出的水流呈抛物线状，测得喷出口高出水面0.8m，水流在离喷出口的水平距离1.25m处达到最高，密集的水滴在水面上形成了一个半径为3m的圆，考虑到出水口过高影响美观，水滴落水形成的圆半径过大容易造成水滴外溅到池外，现决定通过降低出水口的高度，使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面（ ）
A.0.55米B.
米C.
米D.0.4米
【答案】B
【解析】
如图，以O为原点，建立平面直角坐标系，由题意得到对称轴为x＝1.25＝
，A（0，0.8），C（3，0），列方程组求得函数解析式，即可得到结论．
解：如图，以O为原点，建立平面直角坐标系，
由题意得，对称轴为x＝1.25＝，A（0，0.8），C（3，0），
设解析式为y＝ax2+bx+c，
∴
，
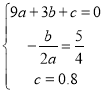解得：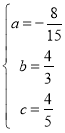
，
所以解析式为：y＝
x2+
x+
，
当x＝2.75时，y＝
，
∴使落水形成的圆半径为2.75m，则应把出水口的高度调节为高出水面08﹣＝
，
故选：B．
练习册系列答案
相关题目
