题目内容
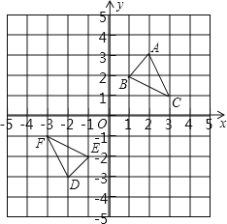
【题目】将一块直角三角板的直角顶点绕着矩形![]() (
(![]() )对角线交点
)对角线交点![]() 旋转(如图①→②→③),
旋转(如图①→②→③),![]() 、
、![]() 分别为直角三角板的直角边与矩形
分别为直角三角板的直角边与矩形![]() 的边
的边![]() 、
、![]() 的交点.
的交点.
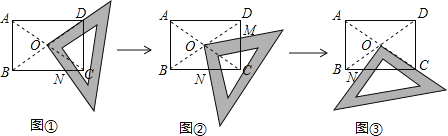
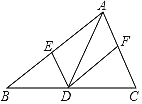
(1)发现:在图①中,当三角板的一直角边与![]() 重合,易证
重合,易证![]() ,
,
证明方法如下:连接![]() ,
,
∵![]() 为矩形
为矩形
∴![]()
又∵![]()
∴![]()
又∵![]()
∴![]()
∴![]()
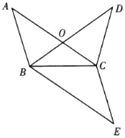
在图③中,当三角板的一直角边与![]() 重合,求证:
重合,求证:![]() .
.
(2)根据以上学习探究:图②中![]() 、
、![]() 、
、![]() 、
、![]() 这四条线段之间的数量关系,写出你的结论,并说明理由.
这四条线段之间的数量关系,写出你的结论,并说明理由.
【答案】(1)见详解;(2)BN2+DM2=CM2+CN2,理由见详解
【解析】
(1)连接![]() ,由中垂线的性质得
,由中垂线的性质得![]() ,由勾股定理得
,由勾股定理得![]() ,进而即可得到结论;
,进而即可得到结论;
(2)延长NO交AD于点P,连接PM,MN,易证△BON≌△DOP,结合中垂线的性质得PM=MN,由勾股定理得PM2=PD2+DM2,MN2=CM2+CN2,进而即可得到结论.
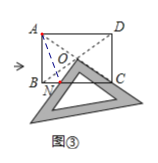
(1)连接![]() ,如图③,
,如图③,
∵四边形![]() 为矩形,
为矩形,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∵AB=CD,
∴![]() ;
;
(2)BN2+DM2=CM2+CN2,理由如下:
如图②,延长NO交AD于点P,连接PM,MN,
∵四边形ABCD是矩形,
∴OD=OB,AD∥BC,
∴∠DPO=∠BNO,∠PDO=∠NBO,
在△BON和△DOP中,
∵ ,
,
∴△BON≌△DOP(AAS),
∴ON=OP,BN=PD,
∵∠MON=90°,即:OM是线段PN的中垂线,
∴PM=MN,
∵∠PDM=∠NCM=90°,
∴PM2=PD2+DM2,MN2=CM2+CN2,
∴PD2+DM2=CM2+CN2,
∴BN2+DM2=CM2+CN2.


【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,下表是试验中的一组统计数据:
摸球的次数 | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数 | 65 | 124 | 178 | 302 | 480 | 601 | 1800 |
摸到白球的频率 |
|
|
|
|
|
|
|
(1)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为______.
(2)试估算盒子里黑、白两种颜色的球各有多少个?