题目内容
已知点A是直线y=-3x+6与y轴的交点,点B在第四象限且在直线y=-3x+6上,线段AB的长度是3| 5 |
(1)若点B1与B关于y轴对称,求点B1的坐标;
(2)若点B1恰好落在x轴上,求sin∠B1AB的值.
分析:(1)欲求点B1的坐标,求出点B坐标即可.过点B作BD⊥Y轴,垂足为D,利用三角形相似就可以求出B的坐标;
(2)欲求sin∠B1AB的值,需构建直角三角形,因此过B1作B1E⊥AC,垂足为E,运用面积法求出B1E即解.
(2)欲求sin∠B1AB的值,需构建直角三角形,因此过B1作B1E⊥AC,垂足为E,运用面积法求出B1E即解.
解答: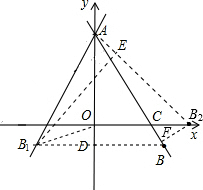 解:(1)如图,设直线y=-3x+6与x轴交于点C,
解:(1)如图,设直线y=-3x+6与x轴交于点C,
则C(2,0).
∴AC=
=2
,
过点B作BD⊥y轴,垂足为D,
∴△AOC∽△ADB,
∴
=
,
∴DB=
=
,
又∵
=
,
∴AD=
=
,
∴OD=
-6,
=
,
∴点B(
,
),
∴点B1(-
,
);
(2)当直线AB绕点A顺时针旋转,点B的对应点落在x负半轴上时,记点B的对应点为B1.
∵AB=3
由旋转的性质可知AB1=AB=3
,
∴B1O=
=3,
B1C=5,
过B1作B1E垂直AC,垂足为E.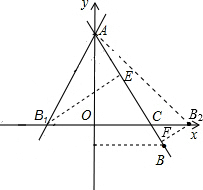
则有
×B1E×AC=
×AO×B1C,
∴B1E=
=
,
在Rt△AB1E中,sin∠B1AB=
=
=
,
当直线AB绕点A逆时针旋转,点B的对应点落在x正半轴上时,记点B的对应点为B2.
则B2O=3,
过B2向AB作垂线B2F,垂足为F.
∵∠B1EC=∠B2FC=90°,∠ECB1=∠FCB2
∴△B1EC∽△B2FC,
∴
=
,
∴FB2=
,
在Rt△AFB2中,sin∠B2AF=
=
=
,
∴sin∠B1AB的值是
或
.
 解:(1)如图,设直线y=-3x+6与x轴交于点C,
解:(1)如图,设直线y=-3x+6与x轴交于点C,则C(2,0).
∴AC=
| 62+22 |
| 10 |
过点B作BD⊥y轴,垂足为D,
∴△AOC∽△ADB,
∴
| AC |
| AB |
| OC |
| DB |
∴DB=
3
| ||
2
|
| 3 |
| 2 |
| 2 |
又∵
| AC |
| AB |
| AO |
| AD |
∴AD=
3
| ||
2
|
| 9 |
| 2 |
| 2 |
∴OD=
| 9 |
| 2 |
| 2 |
=
9
| ||
| 2 |
∴点B(
| 3 |
| 2 |
| 2 |
12-9
| ||
| 2 |
∴点B1(-
| 3 |
| 2 |
| 2 |
12-9
| ||
| 2 |
(2)当直线AB绕点A顺时针旋转,点B的对应点落在x负半轴上时,记点B的对应点为B1.
∵AB=3
| 5 |
由旋转的性质可知AB1=AB=3
| 5 |
∴B1O=
(-
|
B1C=5,
过B1作B1E垂直AC,垂足为E.

则有
| 1 |
| 2 |
| 1 |
| 2 |
∴B1E=
| 6×5 | ||
2
|
| 3 |
| 2 |
| 10 |
在Rt△AB1E中,sin∠B1AB=
| B1E |
| AB1 |
| ||||
3
|
| ||
| 2 |
当直线AB绕点A逆时针旋转,点B的对应点落在x正半轴上时,记点B的对应点为B2.
则B2O=3,
过B2向AB作垂线B2F,垂足为F.
∵∠B1EC=∠B2FC=90°,∠ECB1=∠FCB2
∴△B1EC∽△B2FC,
∴
| B1E |
| FB2 |
| B1C |
| CB2 |
∴FB2=
| 3 |
| 10 |
| 10 |
在Rt△AFB2中,sin∠B2AF=
| B2F |
| AB2 |
| ||||
3
|
| ||
| 10 |
∴sin∠B1AB的值是
| ||
| 2 |
| ||
| 10 |
点评:此题主要考查一次函数的图形和性质、相似三角形判定和性质及三角函数定义,此外还考查了对称和旋转的性质,综合性比较强.

练习册系列答案
相关题目
 如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线.
如图,已知点O是直线AB上的一点,∠BOC=40°,OD、OE分别是∠BOC、∠AOC的角平分线. 已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.
已知点O是直线AB上的一点,∠COE=90°,OF是∠AOE的平分线.