题目内容
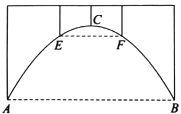
【题目】如图,是某座抛物线型的隧道示意图,已知路面AB宽24米,抛物线最高点C到路面AB的距离为8米,为保护来往车辆的安全,在该抛物线上距路面AB高为6米的点E,F处要安装两盏警示灯,求这两盏灯的水平距离EF.
【答案】12m.
【解析】
利用待定系数法求得抛物线的解析式,已知抛物线上距水面AB高为6米的E、F两点,可知E、F两点纵坐标为6,把y=6代入抛物线解析式,可求E、F两点的横坐标,根据抛物线的对称性求EF长.
解:如图,
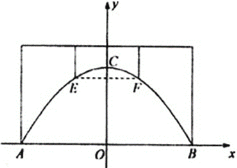
以AB所在直线为x轴、线段AB的中垂线为y轴建立直角坐标系,由题意知,A(-12,0),B(12,0),C(0,8).
设过点A、B、C的抛物线解析式为:
y=ax2+8(a<0).
把点B(12,0)的坐标代入,得a×122+8=0
解得:a=![]() ,
,
则该抛物线的解析式为:![]()
把y=6代入,得![]() ,
,
解得x1=6,x2=-6.
所以两盏警示灯之间的水平距离为:EF=|x1-x2|=|6-(-6)|=12(m).

练习册系列答案
相关题目