题目内容
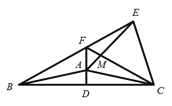
【题目】已知:如图,在等腰三角形ABC中,120BAC180,ABAC,ADBC于点D,以AC为边作等边三角形ACE,ACE与ABC在直线AC的异侧,直线BE交直线AD于点F,连接FC交AE于点M.
(1)求EFC的度数;
(2)求证:FE+FA=FC.
【答案】(1)![]() ;(2)详见解析
;(2)详见解析
【解析】
(1)根据等腰三角形的性质得出∠1=∠2,由直线AD垂直平分BC,求出FB=FC,根据等腰三角形的性质得出∠3=∠4,然后求出AB=AE,根据等腰三角形的性质得出∠3=∠5,等量代换求出![]() 即可得到
即可得到![]() ;
;
(2)在FC上截取FN,使FN=FE,连接EN,根据等边三角形的判定得出△EFN是等边三角形,求出∠FEN=60°,EN=EF,再求出∠5=∠6,根据SAS推出△EFA≌△ENC,根据全等得出FA=NC,即可证得结论.
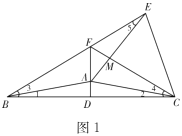
解:(1)如图1,∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴直线![]() 垂直平分
垂直平分![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
∴在等边三角形![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵在等边三角形![]() 中,
中,![]() ,
,
∴![]() ;
;
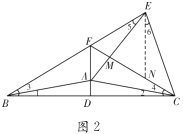
(2)在![]() 上截取
上截取![]() ,使
,使![]() ,连接
,连接![]() ,如图2,
,如图2,
∵![]() ,
,
∵![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() ,
,
在![]() 和
和![]() 中,
中,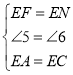 ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
相关题目