Question

【题目】在平面直角坐标系中，如果点、点为某个菱形的一组对角的顶点，且点、在直线上，那么称该菱形为点、的“极好菱形”．如图为点、的“极好菱形”的一个示意图．已知点的坐标为，点的坐标为．

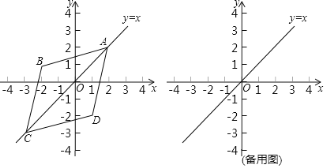
（1）点，，中，能够成为点、的“极好菱形”的顶点的是　 　．

（2）若点、的“极好菱形”为正方形，求这个正方形另外两个顶点的坐标．

（3）如果四边形是点、的“极好菱形”．

①当点的坐标为时，求四边形的面积．

②当四边形的面积为8，且与直线有公共点时，直接写出的取值范围．

Answer 1

【答案】（1），；（2）这个正方形另外两个顶点的坐标为、；（3）①；②的取值范围是

【解析】

（1）根据“极好菱形”的定义判断即可；

（2）根据点、的“极好菱形”为正方形求解即可；

（3）①四边形MNPQ是点M、P的“极好菱形”， 点的坐标为时，求四边形是正方形，求其面积即可；②根据菱形的面积公式求得菱形另一条对角线的长，再由与直线有公共点，求解即可．

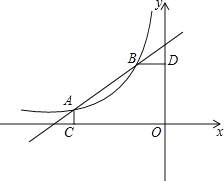
解：（1）如图1中，观察图象可知：、能够成为点，的“极好菱形”顶点．

故答案为：，；

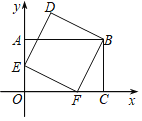
（2）如图2所示：

∵点的坐标为，点的坐标为，

∴．

∵“极好菱形”为正方形，其对角线长为，

∴这个正方形另外两个顶点的坐标为、

（3）①如图2所示：

∵，，，

∴，．

∵四边形是菱形，

∴四边形是正方形．

∴．

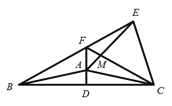
②如图3所示：

∵点的坐标为，点的坐标为，

∴，

∵四边形的面积为8，

∴，即，

∴，

∵四边形是菱形，

∴，，，

作直线，交轴于，

∵，

∴，

∴，

∵和在直线上，

∴，

∴是等腰直角三角形，

∴，

∴与重合，即在轴上，

同理可知：在轴上，且，

由题意得：四边形与直线有公共点时，的取值范围是．