题目内容
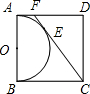 如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则
如图,以正方形ABCD的AB边为直径作半圆O,过点C作直线切半圆于点E,交AD边于点F,则| FE | EC |
分析:连接OE、OF、OC,根据切线长定理证明∠COF=90°;根据切线的性质得OE⊥CF.则△EOF∽△EOC,得EF与EC的关系式,然后求解.
解答: 解:连接OE、OF、OC.
解:连接OE、OF、OC.
∵AD、CF、CB都与⊙O相切,
∴CE=CB;OE⊥CF; OF平分∠AFC,OC平分∠BCF.
∵AF∥BC,
∴∠AFC+∠BCF=180°,
∴∠OFC+∠OCF=90°,
∴∠COF=90°.
∴△EOF∽△EOC,得 OE2=EF•EC.
设正方形边长为a,则OE=
a,CE=a.
∴EF=
a.
∴
=
.
故答案为
.
 解:连接OE、OF、OC.
解:连接OE、OF、OC.∵AD、CF、CB都与⊙O相切,
∴CE=CB;OE⊥CF; OF平分∠AFC,OC平分∠BCF.
∵AF∥BC,
∴∠AFC+∠BCF=180°,
∴∠OFC+∠OCF=90°,
∴∠COF=90°.
∴△EOF∽△EOC,得 OE2=EF•EC.
设正方形边长为a,则OE=
| 1 |
| 2 |
∴EF=
| 1 |
| 4 |
∴
| EF |
| EC |
| 1 |
| 4 |
故答案为
| 1 |
| 4 |
点评:此题考查切线的性质和切线长定理及相似三角形的判定与性质,综合性较强,有相当的难度.

练习册系列答案
相关题目
 13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=
13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=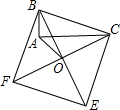 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO= 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( ) 如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )
如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )