题目内容
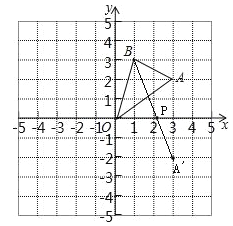
【题目】如图，在边长为1的正方形组成的网格中，△AOB的顶点均在格点上，点A、B的坐标分别是A（3，2），B（1，3）．
（1）求△AOB的面积；
（2）点P在x轴上，当PA+PB的值最小时，在图中画出点P，并求出点P的坐标．
【答案】（1）△AOB的面积为
；
（2）在图中画出点P见解析，点P的坐标为
．
【解析】试题分析：（1）利用三角形所在的矩形的面积减去四周三个小直角三角形的面积列式计算即可得解；（2）找出点A关于x轴的对称点A′位置，连接A′B，根据轴对称确定最短路线问题与x轴的交点即为所求的点P.
试题解析:(1)∵A（3，2），B（1，3）
∴△AOB的面积
(2) ∵A（3，2）, B（1，3）
∴点A关于x轴对称的点A(3,-2)
连接AB与x轴的交点即为满足条件的点P如图所示.
设直线AB为: 
,则
解之得: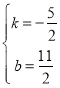 
∴直线AB为: 
当
时
解得
∴满足条件的点P的坐标为
.
练习册系列答案
53随堂测系列答案
相关题目
【题目】某农场引进一批新麦种，在播种前做了五次发芽实验，每次任取800 粒麦种进行实验．实验结果如表所示 （ 发芽率精确到 0.001 ）：
实验的麦种数 | 800 | 800 | 800 | 800 | 800 |
发芽的麦种数 | 787 | 779 | 786 | 789 | 782 |
发芽率 | 0.984 | 0.974 | 0.983 | 0.986 | 0.978 |
在与实验条件相同的情况下，估计种一粒这样的麦种发芽的概率为______．
