题目内容
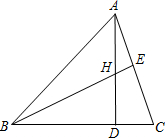 如图,△ABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由.
如图,△ABC的两条高AD、BE相交于H,且AD=BD,试说明下列结论成立的理由.
(1)∠DBH=∠DAC;
(2)BH=AC;
(3)如果BC=14,AH=2,AC=10,求HE的长度.
解:(1)∵AD,BE是△ABC的高
∴∠ADC=∠BEC=90°,
∴∠DBH+∠C=90°,∠DAC+∠C=90°
∴∠DBH=∠DAC;
(2)由(1)题已得∠DBH=∠DAC,
∵在△BDH和△ADC中,
 ,
,
∴△BDH≌△ADC(ASA),
∴BH=AC;
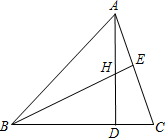
(3)由(2)题已证△BDH≌△ADC,
∴HD=DC(设长度为x)
设AD=BD=y,
∵BC=14,AH=2,AC=10
∴x+y=14,y-x=2.
解得x=6,y=8,
∵ ×AC×BE=
×AC×BE= ×BC×AD,
×BC×AD,
∴10×BE=14×8,
解得BE=11.2,
∴HE=BE-BH=11.2-10=1.2.
分析:(1)求出∠ADC=∠BEC=90°,根据三角形内角和定理得出∠DBH+∠C=90°,∠DAC+∠C=90°,即可求出答案;
(2)求出∠DBH=∠DAC,根据ASA证△BDH≌△ADC,根据全等三角形的性质推出即可;
(3)根据全等三角形性质得出HD=DC,设HD=DC=x,AD=BD=y,得出x+y=14,y-x=2.求出x、y的值,根据三角形面积公式得出 ×AC×BE=
×AC×BE= ×BC×AD,代入求出BE,代入HE=BE-BH求出即可.
×BC×AD,代入求出BE,代入HE=BE-BH求出即可.
点评:本题考查了全等三角形的性质和判定,三角形的内角和定理,三角形的面积等知识点的应用.
∴∠ADC=∠BEC=90°,
∴∠DBH+∠C=90°,∠DAC+∠C=90°
∴∠DBH=∠DAC;
(2)由(1)题已得∠DBH=∠DAC,
∵在△BDH和△ADC中,
 ,
,∴△BDH≌△ADC(ASA),
∴BH=AC;

(3)由(2)题已证△BDH≌△ADC,
∴HD=DC(设长度为x)
设AD=BD=y,
∵BC=14,AH=2,AC=10
∴x+y=14,y-x=2.
解得x=6,y=8,
∵
 ×AC×BE=
×AC×BE= ×BC×AD,
×BC×AD,∴10×BE=14×8,
解得BE=11.2,
∴HE=BE-BH=11.2-10=1.2.
分析:(1)求出∠ADC=∠BEC=90°,根据三角形内角和定理得出∠DBH+∠C=90°,∠DAC+∠C=90°,即可求出答案;
(2)求出∠DBH=∠DAC,根据ASA证△BDH≌△ADC,根据全等三角形的性质推出即可;
(3)根据全等三角形性质得出HD=DC,设HD=DC=x,AD=BD=y,得出x+y=14,y-x=2.求出x、y的值,根据三角形面积公式得出
 ×AC×BE=
×AC×BE= ×BC×AD,代入求出BE,代入HE=BE-BH求出即可.
×BC×AD,代入求出BE,代入HE=BE-BH求出即可.点评:本题考查了全等三角形的性质和判定,三角形的内角和定理,三角形的面积等知识点的应用.

练习册系列答案
相关题目
 如图,△ABC的两条高BD和CE相交于点O,若△DOE的面积为2,△BOC的面积为6,那么cosA=( )
如图,△ABC的两条高BD和CE相交于点O,若△DOE的面积为2,△BOC的面积为6,那么cosA=( )A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 已知:如图,△ABC的两条高BE、CD相交于点O,且OB=OC,求证:△ABC是等腰三角形.
已知:如图,△ABC的两条高BE、CD相交于点O,且OB=OC,求证:△ABC是等腰三角形. 如图,△ABC的两条中线BG、CD相交于点O,点E、F分别是BO、CO的中点.
如图,△ABC的两条中线BG、CD相交于点O,点E、F分别是BO、CO的中点. 如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( )
如图,△ABC的两条角平分线BD、CE交于O,且∠A=60°,则下列结论中不正确的是( ) 如图,△ABC的两条中线AD、BE相交于点G,如果S△ABG=2,那么S△ABC=
如图,△ABC的两条中线AD、BE相交于点G,如果S△ABG=2,那么S△ABC=