题目内容
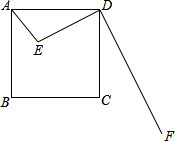如图，已知E是边长为4cm的正方形ABCD内一点，且DE=3，∠AED=90°，DF⊥DE于D，在射线DF上是否存在这样的M，使得以C、D、M为顶点的三角形与△ADE相似？若存在，请求出满足条件的DM长；若不存在，请说明理由．
分析：相似三角形对应角相等，对应边比值相等，故使得△CDM中有一个角为直角即可证明△CDM与△ADE相似，分两种情况①∠DMC=90°、②∠DCM′=90°讨论即可解题．
解答：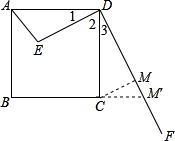
解：∵∠1+∠2=90°∠2+∠3=90°，
∴∠1=∠3，
∵∠AED=90°，
所以使得△CDM中有一个直角即可，
①∠DMC=90°，DM=DE=3cm，
②∠DCM′=90°，
=
，DM′=
cm，
故存在M点，当DM=3cm或
cm时，△CDM与△ADE相似．
解：∵∠1+∠2=90°∠2+∠3=90°，∴∠1=∠3，
∵∠AED=90°，
所以使得△CDM中有一个直角即可，
①∠DMC=90°，DM=DE=3cm，
②∠DCM′=90°，
| DM′ |
| DC |
| DA |
| DE |
| 16 |
| 3 |
故存在M点，当DM=3cm或
| 16 |
| 3 |
点评：本题考查了相似三角形对应边比值相等的性质，相似三角形对应角相等的性质，讨论∠DMC=90°或∠DCM′=90°是解题的关键．
练习册系列答案
阅读快车系列答案
相关题目
匀速运动，其中点P运动的速度是1cm/s，点Q运动的速度是2cm/s，当点Q运动到点C时，P，Q都停止运动．
如图，已知P是边长为2的正方形ABCD的边CD任意一点，且PE⊥DB，垂足为E，PF⊥CA垂足为F，则PE+PF的长是
的坐标为（-1，0）．
A的坐标为（-1，0）．
如图，已知△ABC是边长为2