题目内容
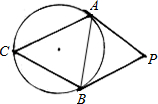16、如图，△ABC内接于⊙O，PA，PB是切线，A、B分别为切点，若∠C=62°，则∠APB=56°
．分析：由于PA、PB都是⊙O的切线，可由弦切角定理求出∠PAB，∠PBA的度数，进而可根据三角形内角和求出∠APB的度数．
解答：解：∵PA、PB分别是⊙O的切线，
∴∠PAB=∠PBA=∠C=62°，
∵∠APB=180°-62°-62°=56°．
故答案为：56°．
∴∠PAB=∠PBA=∠C=62°，
∵∠APB=180°-62°-62°=56°．
故答案为：56°．
点评：此题主要考查了弦切角定理和三角形内角和的综合应用能力．
练习册系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
15、如图，△ABC内接于⊙O，∠BAC=120°，AB=AC=4．BD为⊙O的直径，则BD=
21、如图，△ABC内接于⊙O，AB为⊙O的直径，点D在AB的延长线上，∠A=∠D=30°．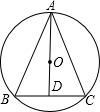
已知：如图，△ABC内接于⊙O，连接AO并延长交BC于点D，若AO=5，BC=8，∠ADB=90°，求△ABC的面积．
18、如图，△ABC内接于⊙O，∠A=30°，若BC=4cm，则⊙O的直径为（ ）
如图，△ABC内接于⊙O，AD⊥BC于点D，求证：∠BAD=∠CAO．