��Ŀ����
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�������OABC�Ķ���O������ԭ���غϣ���C������Ϊ��0��3������A��x��ĸ������ϣ���D��M�ֱ��ڱ�AB��OA�ϣ���AD=2DB��AM=2MO��һ�κ���y=kx+b��ͼ�����D��M������������y= ![]() ��ͼ����D����BC�Ľ���ΪN��
��ͼ����D����BC�Ľ���ΪN�� 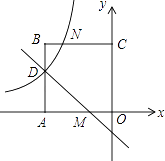
��1������������һ�κ����ı���ʽ��
��2������P��ֱ��DM�ϣ���ʹ��OPM��������ı���OMNC�������ȣ����P�����꣮
���𰸡�
��1���⣺��������OABC�Ķ���C��0��3����
��OA=AB=BC=OC=3����OAB=��B=��BCO=90�㣬
��AD=2DB��
��AD= ![]() AB=2��
AB=2��
��D����3��2����
��D�������y= ![]() �ã�m=��6��
�ã�m=��6��
�෴��������ʽΪy=�� ![]() ��
��
��AM=2MO��
��MO= ![]() OA=1����M����1��0����
OA=1����M����1��0����
��M��D�������y=kx+b�еã� ![]() ��
��
��ã�k=b=��1��
��ֱ��DM����ʽΪy=��x��1
��2���⣺��y=3����y=�� ![]() �ã�x=��2��
�ã�x=��2��
��N����2��3������NC=2��
��P��x��y����
�ߡ�OPM��������ı���OMNC�������ȣ�
�� ![]() ��OM+NC��OC=
��OM+NC��OC= ![]() OM|y|����|y|=9��
OM|y|����|y|=9��
��ã�y=��9��
��y=9ʱ��x=��10����y=��9ʱ��x=8��
��P��������10��9����8����9��
����������1����������OABC�Ķ���C���꣬ȷ�����߳������ĸ���Ϊֱ�ǣ�����AD=2DB�����AD�ij���ȷ����D���꣬���뷴��������ʽ���m��ֵ������AM=2MO��ȷ����MO�ij�����M���꣬��M��D�������һ�κ�������ʽ���k��b��ֵ������ȷ����һ�κ�������ʽ����2����y=3���뷴��������ʽ���x��ֵ��ȷ����N���꣬�õ�NC�ij�����P��x��y�������ݡ�OPM��������ı���OMNC�������ȣ����y��ֵ�������õ�x��ֵ��ȷ����P���꼴�ɣ�

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�