题目内容
【题目】将一块a×b×c的长方体铁块（如图1所示，a＜b＜c，单位：cm）放入一长方体（如图2所示）水槽中，并以速度20cm3/s匀速向水槽注水，直至注满为止．若将铁块a×c面放至水槽的底面，则注水全过程中水槽的水深y （cm）与注水时间t （s）的函数图象如图3所示（水槽各面的厚度忽略不计）．已知a为5cm．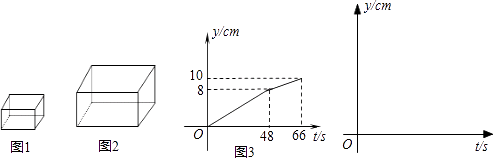 
（1）填空：水槽的深度为cm，b=cm；
（2）求水槽的底面积S和c的值；
（3）若将铁块的b×c面放至水槽的底面，求注水全过程中水槽的水深y（cm）与注水时间t（s）的函数关系，写出t的取值范围，并画出图象．
【答案】
（1）10；8
（2）解：由题意，得
水槽的底面积为；20×（66﹣48）÷（10﹣8），
=380÷2，
=180平方厘米，
水槽铁块占去后的底面积为：48×20÷8=120平方厘米，
∴a×c的面积为：180﹣120=60平方厘米，
即ac=60平方厘米，
∵a=5cm，
∴c=12cm
（3）解：由题意，得
铁块向下面的面积为：bc=12×8=96平方厘米，
∴水槽空出额面积为：180﹣96=84平方厘米，
∴空出部分平铁块高度的体积为：84×5=420立方厘米，
∴注水420立方厘米的水需要的时间是：420÷20=21s，
水槽上部分的体积为：180×5=900立方厘米，
∴注水900立方厘米的水需要的时间是：900÷20=45s，
画图为：
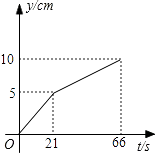
【解析】解：（1）由图象得水槽的深度为10cm，b的值为8cm；通过观察图形可以得出水槽的深度是10cm，b的值就是铁块a×c面向下时的高度为8cm；（2）由注水速度和时间可以求出48秒内注水的体积，除以高度8cm就可以求出没有放铁块部分的面积，根据18s注水体积除以高度就可以得出水槽的底面积，减去空白部分的面积就是铁块a×c面的面积，从而可以求出c的值；（3）根据（1）（2）的结论求出b×c的值就可以求出水槽空出的底面积，由其高度可以求出体积，根据注水速度就可以求出时间，再算出铁块上部分的体积就可以求出时间，从而得出结论．根据题意画出图形．
