题目内容
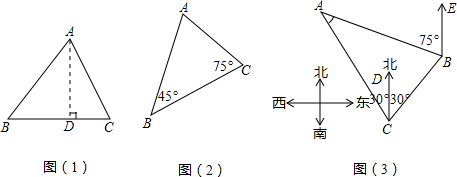
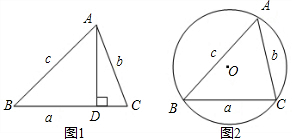
阅读下列材料,并解决后面的问题,在锐角△ABC中,∠A、∠B、∠C的对边分别是a、b、c,则(1)过点A作AD⊥BC于D(如图1),
则在Rt△ABD中,AD=
在Rt△ACD中,AD=
∴
∴
同理最后可得,
(2)用尺规画△ABC的外接圆⊙O,半径为r(图2),请你另用不同的方法证明以上结论;并写出上述结论与△ABC外接圆直径的关系.
(3)应用:△ABC中,若∠A=30°,∠B=45°,b=
| 2 |
分析:(1)根据正弦的定义写出,然后再等量代换进行整理;
(2)过点C作直径交⊙O于点D,连接BD,根据同弧所对的圆周角相等可得∠D=∠A,直径所对的圆周角是直角可得∠DBC=90°,在Rt△BDC中表示出sinD,也就是sinA,然后代入
整理即可,同理可证其它两个也成立;
(3)代入上述结论计算即可.
(2)过点C作直径交⊙O于点D,连接BD,根据同弧所对的圆周角相等可得∠D=∠A,直径所对的圆周角是直角可得∠DBC=90°,在Rt△BDC中表示出sinD,也就是sinA,然后代入
| a |
| sinA |
(3)代入上述结论计算即可.
解答:(1)解:AD=c•sinB,
AD=b•sinC,
c•sinB=b•sinC,
=
,
同理可得:
=
=
;
(2)证明:如图,点C作直径CD交⊙O于点D,连接BD,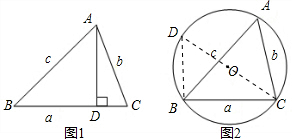
∴∠A=∠D(同弧所对的圆周角相等),
∠DBC=90°(直径所对的圆周角是直角),
∴sinA=sinD,sinD=
,
∴
=
=2r,
同理可证:
=2r,
=2r,
∴
=
=
=2r;
(3)解:∵
=
,∠A=30°,∠B=45°,b=
,
∴
=
,
解得a=
×
=1,
∵
=2r,
∴
=2r,
解得r=1,
故答案为:a=1,r=1.
AD=b•sinC,
c•sinB=b•sinC,
| b |
| sinB |
| c |
| sinC |
同理可得:
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
(2)证明:如图,点C作直径CD交⊙O于点D,连接BD,

∴∠A=∠D(同弧所对的圆周角相等),
∠DBC=90°(直径所对的圆周角是直角),
∴sinA=sinD,sinD=
| a |
| 2r |
∴
| a |
| sinA |
| a | ||
|
同理可证:
| b |
| sinB |
| c |
| sinC |
∴
| a |
| sinA |
| b |
| sinB |
| c |
| sinC |
(3)解:∵
| a |
| sinA |
| b |
| sinB |
| 2 |
∴
| a |
| sin30° |
| ||
| sin45° |
解得a=
| 2 |
| ||||
|
∵
| b |
| sinB |
∴
| ||
| sin45° |
解得r=1,
故答案为:a=1,r=1.
点评:本题考查了解直角三角形,主要利用了正弦的定义,(2)的证明作出辅助性,构造出以直径为斜边的直角三角形是解题的关键,也是难点,希望同学们要多动脑筋,从题目的条件与结论入手考虑问题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
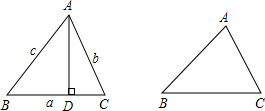 阅读下列材料,并解决后面的问题.
阅读下列材料,并解决后面的问题. nB,AD=bsinC,于是csinB=bsinC,即
nB,AD=bsinC,于是csinB=bsinC,即 到0.1.参考数据:sin40°=0.643,sin65°=0.90 6,sin70°=0.940,sin75°=0.966).
到0.1.参考数据:sin40°=0.643,sin65°=0.90 6,sin70°=0.940,sin75°=0.966).