��Ŀ����
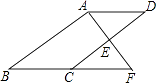
����Ŀ����ƽ��ֱ������ϵ�У�����������y= ![]() ��x��0����ͼ������һ��A��a��3��������A��AB��x���ڵ�B������B��x��������ƽ��2����λ���ȵõ���C������C��y���ƽ���߽������������ڵ�D��CD=
��x��0����ͼ������һ��A��a��3��������A��AB��x���ڵ�B������B��x��������ƽ��2����λ���ȵõ���C������C��y���ƽ���߽������������ڵ�D��CD= ![]() ��ֱ��AD��x�ύ�ڵ�M����y�ύ�ڵ�N��
��ֱ��AD��x�ύ�ڵ�M����y�ύ�ڵ�N��
��1���ú�a��ʽ�ӱ�ʾ��D�ĺ�����Ϊ����
��2����a��ֵ��ֱ��AD�ĺ�������ʽ��
��3�����ж��߶�AN��MD��������ϵ����˵�����ɣ�
��4����һ�κ���y1=k1x+b1�����㣨10��9������˫����y= ![]() ��x��0�����ڵ�P���Ҹ�һ�κ���y1��ֵ��x�������������ȷ��P�������n��ȡֵ��Χ������д�����̣�
��x��0�����ڵ�P���Ҹ�һ�κ���y1��ֵ��x�������������ȷ��P�������n��ȡֵ��Χ������д�����̣�
���𰸡�
��1��a+2
��2���⣺��CD��y�ᣬ��CD= ![]() ��
��
��D��a+2�� ![]() ����
����
��A��D���ڷ���������ͼ���ϣ�
��  �����
����� ![]() ����a��ֵΪ2��
����a��ֵΪ2��
��A��2��3����D��4�� ![]() ����
����
��ֱ��AD�ĺ�������ʽΪy=kx+b��
��A��D���������ɵ� 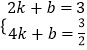 �����
�����  ��
��
��ֱ��AD�ĺ�������ʽΪy=�� ![]() x+
x+ ![]() ��
��
��3���⣺���ۣ�AN=MD��
���ɣ���y=�� ![]() x+
x+ ![]() �У���y=0�ɵ�x=6����x=0�ɵ�y=
�У���y=0�ɵ�x=6����x=0�ɵ�y= ![]() ��
��
��M��6��0����N��0�� ![]() ����
����
��A��2��3����D��4�� ![]() ����
����
��AN= ![]() =
= ![]() ��MD=
��MD= ![]() =
= ![]() ��
��
��AN=MD��
��4���⣺��ͼ����ֱ����x��ֱʱn��ֵ���ֱ����x��ƽ��ʱn��ֵ��С��

��ֱ�ߴ�ֱx��ʱ�����֪E�������Ϊ10������ʱn��ֵΪ10��
��ֱ��ƽ��x��ʱ����F���������Ϊ9���ɣ�1���ɵ÷�������������ʽΪy= ![]() ����y=9ʱ���ɽ��x=
����y=9ʱ���ɽ��x= ![]() ����P��ĺ�����Ϊ
����P��ĺ�����Ϊ ![]() ������ʱn��ֵΪ
������ʱn��ֵΪ ![]() ��
��
��һ�κ���y1��ֵ��x�����������
��ֱ����ֱ��P1E��ֱ��P2F֮�䣬
��n��ȡֵ��ΧΪ ![]() ��n��10��
��n��10��
���������⣺��1����A��a��3����AB��x���ڵ�B��
��OB=a��
�߽���B��x��������ƽ��2����λ���ȵõ���C��
��OC=OB+BC=2+a����D��ĺ�����Ϊa+2��
���Դ��ǣ�a+2��

 ��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�
��ĩ���100�ִ��½����ȫ�Ծ�ϵ�д�