��Ŀ����
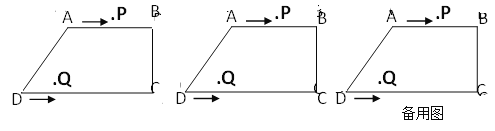
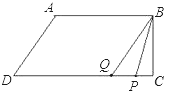
����Ŀ����ֱ������ABCD�У�AB��CD����BCD=90�㣬AB=AD=10cm��BC=8cm����P�ӵ�A��������ÿ��3cm���ٶ�������ABCD�˶�����Q�ӵ�D��������ÿ��2cm���ٶ����߶�DC�������C�˶�����֪����P��Qͬʱ����������Q�˶�����Cʱ��P��Q�˶�ֹͣ�����˶�ʱ��Ϊt��.
��1����CD�ij�.
��2��tΪ��ֵʱ���ı���PBQDΪƽ���ı���.
��3���ڵ�P����Q���˶������У��Ƿ����ijһʱ�̣�ʹ����BPQ�����Ϊ20cm2�������ڣ��������������������t��ֵ���������ڣ���˵������.
���𰸡���1��16����2��![]() ����3��
����3��![]() .
.
�������������������1������A��AM��CD��M���ı���AMCB�Ǿ��Σ�AM=BC,AD����֪�ģ����ݹ��ɶ������DM,CM=AB,����CD��������ˣ���2�����ı���PBQDΪƽ���ı���ʱ,��P��AB�ϣ���Q��DC�ϣ���t��ʾ��BP,DQ�ij�������BP=DQ,���tֵ����BP,DQ���������Ȼ�����CQ,�ù��ɶ������BQ���ı���PBQD���ܳ���������ˣ���3��D��Q��C��Ҫ8�룬����t�ķ�Χ��0��t��8,Q����P�����߶β�ͬ��������������ۣ���������P���߶�AB��ʱ����![]() ʱ����t��ʾ��BP�ij�����������BPQ���������20�ķ�����⣻������P���߶�BC��ʱ����
ʱ����t��ʾ��BP�ij�����������BPQ���������20�ķ�����⣻������P���߶�BC��ʱ����![]() ʱ����t��ʾ��BP,CQ�ij�������������BPQ���������20�ķ�����⣻������P���߶�CD��ʱ����Ϊ����������ʱ����
ʱ����t��ʾ��BP,CQ�ij�������������BPQ���������20�ķ�����⣻������P���߶�CD��ʱ����Ϊ����������ʱ����![]() ������P��Q���Ҳ࣬��6��t��
������P��Q���Ҳ࣬��6��t��![]() ����t��ʾ��PQ�ij��������г��������ʽ��⣻����P��Q����࣬��
����t��ʾ��PQ�ij��������г��������ʽ��⣻����P��Q����࣬��![]() ����t��ʾ��PQ�ij����г��������ʽ��⣮
����t��ʾ��PQ�ij����г��������ʽ��⣮
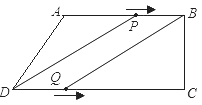
�����������1������A��AM��CD��M�����ݹ��ɶ�����AD=10��AM=BC=8����DM=![]() =6����CD=16����2�����ı���PBQDΪƽ���ı���ʱ����P��AB�ϣ���Q��DC�ϣ���ͼ������֪��AP=3t,BP=10��3t��DQ=2t����10��3t=2t�����t=2����ʱ��BP=DQ=4��CQ=12����
=6����CD=16����2�����ı���PBQDΪƽ���ı���ʱ����P��AB�ϣ���Q��DC�ϣ���ͼ������֪��AP=3t,BP=10��3t��DQ=2t����10��3t=2t�����t=2����ʱ��BP=DQ=4��CQ=12����![]() �����ı���PBQD���ܳ�=2��BP+BQ��=
�����ı���PBQD���ܳ�=2��BP+BQ��=![]() ��
��
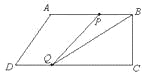
��3��������P���߶�AB��ʱ����B��ʱ��![]() �룬��
�룬��![]() ʱ����ͼ��BP=10��3t��BC=8����
ʱ����ͼ��BP=10��3t��BC=8����![]() ����
����![]() ��
��
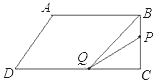
������P���߶�BC��ʱ��P����C��tֵʱ6�룬��![]() ʱ����ͼ��BP=AB+BP-AB=3t��10��DQ=2t,CQ=16��2t����
ʱ����ͼ��BP=AB+BP-AB=3t��10��DQ=2t,CQ=16��2t����![]() ������ã�3t2��34t+100=0����=��44��0�����Է�����ʵ���⣮�������������������BPQ�������20��
������ã�3t2��34t+100=0����=��44��0�����Է�����ʵ���⣮�������������������BPQ�������20��
������P���߶�CD��ʱ��P����Q������ʱ,����2t+3t=10+8+16,t=![]() ,����ʱ����
,����ʱ����![]() ������P��Q���Ҳ࣬��6��t��
������P��Q���Ҳ࣬��6��t��![]() ������PQ=34-��2t+3t��=34��5t������
������PQ=34-��2t+3t��=34��5t������![]() ����˷��̵ã�
����˷��̵ã�
![]() ��6����ȥ������P��Q����࣬��
��6����ȥ������P��Q����࣬��![]() ������PQ=2t+3t-34=5t��34�����з��̣�
������PQ=2t+3t-34=5t��34�����з��̣�![]() ����ã�t=7��8�����ۺϵó�����������tֵ���ڣ���ֵ�ֱ�Ϊ
����ã�t=7��8�����ۺϵó�����������tֵ���ڣ���ֵ�ֱ�Ϊ![]() ��t2=7��8��
��t2=7��8��

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�����Ŀ������ij��ѧ�������й���У�����������ִ������������в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ4��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���