题目内容
【题目】如图,AD是△ABC的角平分线,DE、DF分别是△ABD和△ACD的高。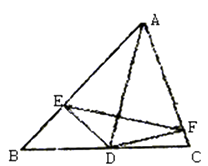
(1)求证:AD垂直平分EF。
(2)若AB+AC=16,S△ABC=24,∠EDF=120°,求AD的长。
【答案】
(1)证明:设 ![]() 的交点为K,
的交点为K,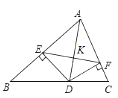
∵AD平分 ![]()
![]()
![]()
![]()
在 ![]() 和
和 ![]() 中,
中,![]() ,
,
∴ ![]() ≌
≌ ![]()
![]()
![]()
又 ![]()
∴ ![]() ≌
≌ ![]()
![]()
![]() 是线段EF的垂直平分线
是线段EF的垂直平分线
(2)解: ![]()
![]()
![]()
![]()
![]()
在四边形AEDF中, ![]()
![]()
![]()
在 ![]() 中,
中, ![]()
【解析】 (1)根据已知条件易证明DE=DF,再通过证明Rt△ADE ≌ Rt△ADF,得到AE=AF,根据到线段两端点距离相等的点在线段的垂直平分线即可证得结论。或证EK=KF,∠AKE=∠AKF=90,也可证得结论。
(2)抓住已知条件AB+AC=16,S△ABC=24,根据三角形的面积公式先求出DE的长,再根据∠EDF的度数求出∠EAD的度数,然后在 Rt△ADE 中,根据30°角所对的直角边等于斜边的一半,求出AD即可。

 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
【题目】小林在某商店购买商品A、B共三次,只有一次购买时,商品A、B同时打折(折扣相同),其余两次均按标价购买.三次购买商品A、B的数量和费用如下表:
购买商品A的数量/个 | 购买商品B的数量/个 | 购买总费用/元 | |
第一次购物 | 6 | 5 | 1140 |
第二次购物 | 3 | 7 | 1110 |
第三次购物 | 9 | 8 | 1062 |
(1)小林以折扣价购买商品A、B是第 次购物;
(2)求出商品A、B的标价;
(3)若商品A、B的折扣相同,问商店是打几折出售这两种商品的?