题目内容
有一座抛物线型拱桥,其水面宽AB为18米,拱顶O离水面AB的距离OM为8米,货船在水面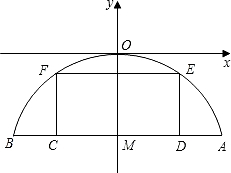 上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.(1)求此抛物线的解析式;
(2)如果限定矩形的长CD为9米,那么矩形的高DE不能超过多少米,才能使船通过拱桥;
(3)若设EF=a,请将矩形CDEF的面积S用含a的代数式表示,并指出a的取值范围.
分析:(1)根据题意设抛物线的解析式为y=ax2+bx+c(a≠0).把已知坐标(-9,-8),(9,-8),(0,0)代入解析式求得a=-
,b=0,c=0.故抛物线的解析式为y=-
x2.
(2)已知CD=9,把已知坐标代入函数关系式可求解.
(3)已知EF=a,易求出E点坐标以及ED的表示式.易求矩形CDEF的面积.
| 8 |
| 81 |
| 8 |
| 81 |
(2)已知CD=9,把已知坐标代入函数关系式可求解.
(3)已知EF=a,易求出E点坐标以及ED的表示式.易求矩形CDEF的面积.
解答:解:(1)y=-
x2(-9≤x≤9)(2分)
(2)∵CD=9
∴点E的横坐标为
,则点E的纵坐标为-
×(
)2=-2
∴点E的坐标为(
,-2),
因此要使货船能通过拱桥,则货船最大高度不能超过8-2=6(米)(5分)
(3)由EF=a,则E点坐标为(
a,-
a2),
此时ED=8-|-
a2|=8-
a2
∴S矩形CDEF=EF•ED=8a-
a3(0<a<18).(7分)
| 8 |
| 81 |
(2)∵CD=9
∴点E的横坐标为
| 9 |
| 2 |
| 8 |
| 81 |
| 9 |
| 2 |
∴点E的坐标为(
| 9 |
| 2 |
因此要使货船能通过拱桥,则货船最大高度不能超过8-2=6(米)(5分)
(3)由EF=a,则E点坐标为(
| 1 |
| 2 |
| 2 |
| 81 |
此时ED=8-|-
| 2 |
| 81 |
| 2 |
| 81 |
∴S矩形CDEF=EF•ED=8a-
| 2 |
| 81 |
点评:本题考查的是二次函数的实际应用以及矩形面积的运算.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
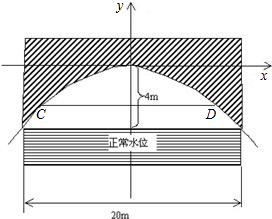 有一座抛物线型拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.
有一座抛物线型拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.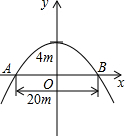 有一座抛物线型拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m.
有一座抛物线型拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m.