题目内容
有一座抛物线型拱桥(图1),其水面宽为18米,拱顶离水面AB的距离为9米.有一货船要将打包好的一些长方体物品(长、宽、高分别是4米、3米、8米)放在甲板上运过拱桥(假设载货后船的甲板与水面大致平齐).(1)求抛物线的解析式.
(2)若货物堆放方式的正视图如下(图2),问船能载货物通过拱桥吗?通过计算说明你的结论.

(3)若改变货物的堆放方式(正视图如图甲、图乙).问图甲和图乙能否载货物通过拱桥?假设此货船的甲板只能提供宽13米,长18米的置物空间,为了尽可能地多装这些长方体物品(略去其它因素),你会选用图甲和图乙中的哪一种载物方式,为什么?
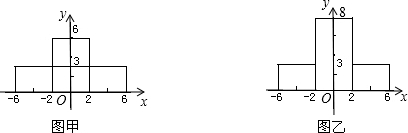
分析:(1)设出函数的关系式,分别根据已知条件求得点A和点B的坐标代入函数解析式求得即可.
(2)将x=4代入函数关系式后求得函数值与8比较即可得到答案;
(3)分别将x=6代入到两个图形中,均能通过,然后根据两船的载货量确定答案即可.
(2)将x=4代入函数关系式后求得函数值与8比较即可得到答案;
(3)分别将x=6代入到两个图形中,均能通过,然后根据两船的载货量确定答案即可.
解答:解:(1)∵水面宽18米,拱顶离水面AB的距离为9米.
∴点A和点B的坐标为(-9,0)和(0,9),
设函数关系式为y=ax2+c,
∴
∴
∴y=-
x2+9.
(2)当x=4时,y≈7.2<8;不能通过.
(3)图甲:当x=2时,y≈8.5>6,
当x=6时,y=5>3,
能通过;
图乙:∵x=2时,y≈8.5>8,
当x=6时,y=5>3,
能通过.
当甲只能运8件物品,而乙能运10件物品,所以选用图乙的载货方式较好.
∴点A和点B的坐标为(-9,0)和(0,9),
设函数关系式为y=ax2+c,
∴
|
∴
|
∴y=-
| 1 |
| 9 |
(2)当x=4时,y≈7.2<8;不能通过.
(3)图甲:当x=2时,y≈8.5>6,
当x=6时,y=5>3,
能通过;
图乙:∵x=2时,y≈8.5>8,
当x=6时,y=5>3,
能通过.
当甲只能运8件物品,而乙能运10件物品,所以选用图乙的载货方式较好.
点评:本题考查了二次函数的应用,还结合了三视图的知识,综合考查了学生们的识图能力,是一道较好的函数应用题.

练习册系列答案
相关题目
 上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.
上的部分的横断面是矩形CDEF,如图建立平面直角坐标系.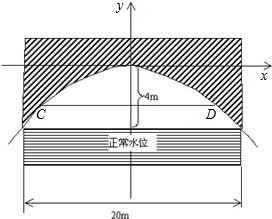 有一座抛物线型拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.
有一座抛物线型拱桥,正常水位时,桥下水面宽度为20m,拱顶距水面4m.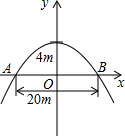 有一座抛物线型拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m.
有一座抛物线型拱桥(如图),正常水位时桥下河面宽20m,河面距拱顶4m.