题目内容
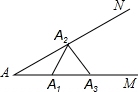 如图,∠MAN=16°,A1点在AM上,在AN上取一点A2,使A2A1=AA1,再在AM上取一点A3使A3A2=A2A1,如此一直作下去,到不能再作为止.那么作出的最后一点是
如图,∠MAN=16°,A1点在AM上,在AN上取一点A2,使A2A1=AA1,再在AM上取一点A3使A3A2=A2A1,如此一直作下去,到不能再作为止.那么作出的最后一点是
- A.A5
- B.A6
- C.A7
- D.A8
B
分析:根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可分别求角另一等腰三角形中的底角与∠A的关系,最后根据三角形内角和定理进行验证不难求解.
解答: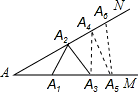 解:∵AA1=A1A2,
解:∵AA1=A1A2,
∴∠AA2A1=∠A,
∵∠A2A1A3=2∠A,∠A=16°,
∴∠A2A1A3=32°,
∵A1A2=A2A3,
∴∠A2A3A=∠A2A1A3=2∠A,
∴∠NA2A3=3∠A=48°,
同理:∠A4A3M=4∠A=64°,∠NA4A5=5∠A=80°,∠NA6A5=6∠A=96°,
∵如果存在A7点,则△A5A6A7为等腰三角形且∠NA6A5是△A5A6A7的一个底角,而∠NA6A5>90°,
∴此假设不成立,即A7点不存在,
∴作出的最后一点为A6,
故选B.
点评:此题主要考查等腰三角形的性质,三角形外角和性质及三角形内角和定理的综合运用.
分析:根据等腰三角形的性质可得到几组相等的角,再根据三角形外角的性质可分别求角另一等腰三角形中的底角与∠A的关系,最后根据三角形内角和定理进行验证不难求解.
解答:
 解:∵AA1=A1A2,
解:∵AA1=A1A2,∴∠AA2A1=∠A,
∵∠A2A1A3=2∠A,∠A=16°,
∴∠A2A1A3=32°,
∵A1A2=A2A3,
∴∠A2A3A=∠A2A1A3=2∠A,
∴∠NA2A3=3∠A=48°,
同理:∠A4A3M=4∠A=64°,∠NA4A5=5∠A=80°,∠NA6A5=6∠A=96°,
∵如果存在A7点,则△A5A6A7为等腰三角形且∠NA6A5是△A5A6A7的一个底角,而∠NA6A5>90°,
∴此假设不成立,即A7点不存在,
∴作出的最后一点为A6,
故选B.
点评:此题主要考查等腰三角形的性质,三角形外角和性质及三角形内角和定理的综合运用.

练习册系列答案
相关题目
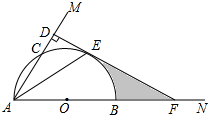 已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F.若cos∠MAN=
已知:如图,在锐角∠MAN的边AN上取一点B,以AB为直径的半圆O交AM于C,交∠MAN的角平分线于E,过点E作ED⊥AM,垂足为D,反向延长ED交AN于F.若cos∠MAN= 如图,∠MAN=16°,A1点在AM上,在AN上取一点A2,使A2A1=AA1,再在AM上取一点A3使A3A2=A2A1,如此一直作下去,到不能再作为止.那么作出的最后一点是( )
如图,∠MAN=16°,A1点在AM上,在AN上取一点A2,使A2A1=AA1,再在AM上取一点A3使A3A2=A2A1,如此一直作下去,到不能再作为止.那么作出的最后一点是( )