题目内容
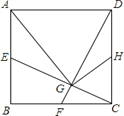
【题目】如图，在
中，
，点
在
上，以
为半径的
交
于点
，
的垂直平分线交
于点
，交于点
，连接
．
（1）判断直线与的位置关系，并说明理由；
（2）若
，
，
，求线段的长．
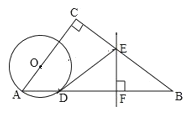
【答案】（1）直线
与
相切；理由见解析；（2）
．
【解析】
（1）连接OD，由OD=OA，利用等边对等角得到一对角相等，再由EF垂直平分BD得DE=BE，得出
，通过
和等量代换可得到∠ODE为直角，即可得证；
（2）连接OE，设DE=x，则EB=ED=x，CE=8x，在直角三角形OCE中，利用勾股定理列出关于x的方程，解方程得到x的值，即可确定出DE的长．
解：（1）直线与相切，理由如下：
如图，连接
，
，
．
是
的垂直平分线，
，
．
，
，
．
．
又
为的半径，
与相切；
（2）如图，连接
∵
，
，
，
∴
，
，
设
，则
，
，
，
，
．
解得
，即．
练习册系列答案
名校课堂系列答案
相关题目
【题目】某商场计划购进
，
两种新型节能台灯共100盏，这两种台灯的进价、售价如下表：
类型 | 价格 | 进价（元/盏） | 售价（元/盏） |
| 30 | 45 | |
| 50 | 70 | |
（1）若设商场购进型台灯
盏，销售完这批台灯所获利润为
，写出与之间的函数关系式；
（2）若商场规定型灯的进货数量不超过型灯数量的4倍，那么型和型台灯各进多少盏售完之后获得利润最多？此时利润是多少元．
