题目内容
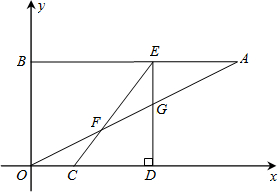
如图,是3×4的正方形网格(每个小正方形的边长为1),点A、B、C、D、E、F、G七点在各点上.

请解答下列各题:
(1)在图(1)中画一个面积为1的直角三角形(三角形的顶点从以上七个点中选择),并将你所画的三角形向左平移2个单位,向上平移1个单位(用阴影表示);
(2)在图(2)中画一个面积为
的钝角三角形(三角形的顶点从以上七个点中选择);
(3)在以上七点中选择三点作为三角形的顶点,其中面积为3的三角形有

请解答下列各题:
(1)在图(1)中画一个面积为1的直角三角形(三角形的顶点从以上七个点中选择),并将你所画的三角形向左平移2个单位,向上平移1个单位(用阴影表示);
(2)在图(2)中画一个面积为
| 1 | 2 |
(3)在以上七点中选择三点作为三角形的顶点,其中面积为3的三角形有
5
5
个.分析:(1)根据面积是1,作两直角边分别是1、2的直角三角形,再根据平移的方法只能是取CG、DG,然后根据平移的性质找出C、G平移后的对应点C′、G′的位置,顺次连接即可;
(2)画出底边与高都是1的钝角三角形即可;
(3)根据面积是3,所作三角形的底边与高的长分别是2、3两个数即可.
(2)画出底边与高都是1的钝角三角形即可;
(3)根据面积是3,所作三角形的底边与高的长分别是2、3两个数即可.
解答: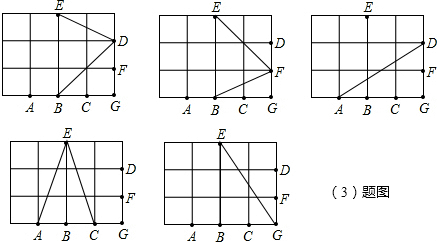 解:(1)所作三角形如图(1)所示;
解:(1)所作三角形如图(1)所示;
(2)如图2所示,△CDF的面积是
,还可以作△ABF、△BCF;
(3)如图所示,△BDE、△BFE、△ADG、△ACE、△BGE的面积都是3,共有5个.

 解:(1)所作三角形如图(1)所示;
解:(1)所作三角形如图(1)所示;(2)如图2所示,△CDF的面积是
| 1 |
| 2 |
(3)如图所示,△BDE、△BFE、△ADG、△ACE、△BGE的面积都是3,共有5个.

点评:本题考查了利用平移变换作图,三角形的面积,根据三角形的面积以及网格结构确定出三角形顶点的位置是解题的关键.

练习册系列答案
相关题目
 4,6),且AB=
4,6),且AB= 13、如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在个点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).
13、如图,方格纸中的每个小方格都是边长为1个单位的正方形,Rt△ABC的顶点均在个点上,在建立平面直角坐标系后,点A的坐标为(-6,1),点B的坐标为(-3,1),点C的坐标为(-3,3).