题目内容
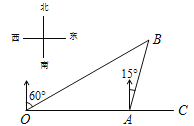
【题目】如图,港口A在观测站O的正东方向,OA=40海里,某船从港口A出发,沿北偏东15°方向航行半小时后到达B处,此时从观测站O处测得该船位于北偏东60°的方向.求该船航行的速度.
【答案】![]()
【解析】
试题分析:过点A作AD⊥OB于D,先解Rt△AOD,得出AD=![]() OA=2海里,再由△ABD是等腰直角三角形,得出BD=AD=2海里,则AB=
OA=2海里,再由△ABD是等腰直角三角形,得出BD=AD=2海里,则AB=![]() AD=
AD=![]() 海里,结合航行时间来求航行速度.
海里,结合航行时间来求航行速度.
试题解析:过点A作AD⊥OB于点D.
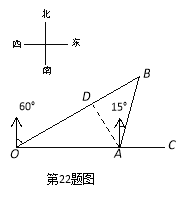
在Rt△AOD中,
∵∠ADO=90°,∠AOD=30°,OA=40,
∴AD=![]() OA=20.
OA=20.
在Rt△ABD中,
∵∠ADB=90°,∠B=∠CAB﹣∠AOB=75°﹣30°=45°
∴∠BAD=180°﹣∠ADB﹣∠B =45°=∠B,
∴BD=AD=20,
∴![]() .
.
∴该船航行的速度为![]() 海里/小时,
海里/小时,
答:该船航行的速度为![]() 海里/小时.
海里/小时.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
【题目】某校开展了主题为“梅山文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问 卷调查的结果分为“非常了解”、“比较了解”、“基本了解”、“不太了解”四个等级,整理调查数据制成 了不完整的表格和扇形统计图(如图).
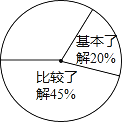
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |
根据以上提供的信息解答下列问题:
(1)本次问卷调查共抽取的学生数为 人,表中m的值为 ;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生2000人,请根据调查结果估计这些学生中“不太了解”梅山文化知识的人数约为多少?