题目内容
【题目】如图1,在菱形ABCD中,AB=6 ![]() ,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
,tan∠ABC=2,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CF.
(1)求证:BE=DF;
(2)当t=秒时,DF的长度有最小值,最小值等于;
(3)如图2,连接BD、EF、BD交EC、EF于点P、Q,当t为何值时,△EPQ是直角三角形?
(4)如图3,将线段CD绕点C顺时针旋转一个角α(α=∠BCD),得到对应线段CG.在点E的运动过程中,当它的对应点F位于直线AD上方时,直接写出点F到直线AD的距离y关于时间t的函数表达式.
【答案】
(1)
解:∵∠ECF=∠BCD,即∠BCE+∠DCE=∠DCF+∠DCE,
∴∠DCF=∠BCE,
∵四边形ABCD是菱形,
∴DC=BC,
在△DCF和△BCE中,
∵  ,
,
∴△DCF≌△BCE(SAS),
∴DF=BE
(2)6 ![]() +6;12
+6;12
(3)
解:∵CE=CF,
∴∠CEQ<90°,
①当∠EQP=90°时,如图2①,

∵∠ECF=∠BCD,BC=DC,EC=FC,
∴∠CBD=∠CEF,
∵∠BPC=∠EPQ,
∴∠BCP=∠EQP=90°,
∵AB=CD=6 ![]() ,tan∠ABC=tan∠ADC=2,
,tan∠ABC=tan∠ADC=2,
∴DE=6,
∴t=6秒;
②当∠EPQ=90°时,如图2②,

∵菱形ABCD的对角线AC⊥BD,
∴EC与AC重合,
∴DE=6 ![]() ,
,
∴t=6 ![]() 秒
秒
(4)
解:y= ![]() t﹣12﹣
t﹣12﹣ ![]() ,
,
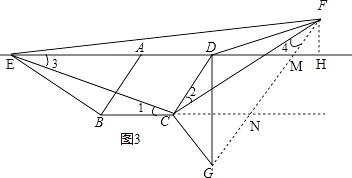
如图3,连接GF分别交直线AD、BC于点M、N,过点F作FH⊥AD于点H,
由(1)知∠1=∠2,
又∵∠1+∠DCE=∠2+∠GCF,
∴∠DCE=∠GCF,
在△DCE和△GCF中,
∵ 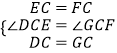 ,
,
∴△DCE≌△GCF(SAS),
∴∠3=∠4,
∵∠1=∠3,∠1=∠2,
∴∠2=∠4,
∴GF∥CD,
又∵AH∥BN,
∴四边形CDMN是平行四边形,
∴MN=CD=6 ![]() ,
,
∵∠BCD=∠DCG,
∴∠CGN=∠DCN=∠CNG,
∴CN=CG=CD=6 ![]() ,
,
∵tan∠ABC=tan∠CGN=2,
∴GN=12,
∴GM=6 ![]() +12,
+12,
∵GF=DE=t,
∴FM=t﹣6 ![]() ﹣12,
﹣12,
∵tan∠FMH=tan∠ABC=2,
∴FH= ![]() (t﹣6
(t﹣6 ![]() ﹣12),
﹣12),
即y= ![]() t﹣12﹣
t﹣12﹣ ![]()
【解析】解:(2)如图1,
当点E运动至点E′时,DF=BE′,此时DF最小,
在Rt△ABE′中,AB=6 ![]() ,tan∠ABC=tan∠BAE′=2,
,tan∠ABC=tan∠BAE′=2,
∴设AE′=x,则BE′=2x,
∴AB= ![]() x=6
x=6 ![]() ,
,
则AE′=6
∴DE′=6 ![]() +6,DF=BE′=12,
+6,DF=BE′=12,
所以答案是:6 ![]() +6,12;
+6,12;
【考点精析】利用菱形的性质对题目进行判断即可得到答案,需要熟知菱形的四条边都相等;菱形的对角线互相垂直,并且每一条对角线平分一组对角;菱形被两条对角线分成四个全等的直角三角形;菱形的面积等于两条对角线长的积的一半.

【题目】为了了解“通话时长”(“通话时长”指每次通话时间)的分布情况,小强收集了他家1000个“通话时长”数据,这些数据均不超过18(分钟).他从中随机抽取了若干个数据作为样本,统计结果如下表,并绘制了不完整的频数分布直方图. 
“通话时长” | 0<x≤3 | 3<x≤6 | 6<x≤9 | 9<x≤12 | 12<x≤15 | 15<x≤18 |
次数 | 36 | a | 8 | 12 | 8 | 12 |
根据表、图提供的信息,解答下面的问题:
(1)a= , 样本容量是;
(2)求样本中“通话时长”不超过9分钟的频率:;
(3)请估计小强家这1000次通话中“通话时长”超过15分钟的次数.