题目内容
【题目】已知二次函数y＝－(a＋b)x2－2cx＋a－b，a、b、c是△ABC的三边
(1) 当抛物线与x轴只有一个交点时，判断△ABC是什么形状
(2) 当
时，该函数有最大值
，判断△ABC是什么形状
【答案】(1) △ABC是以b为斜边的直角三角形;(2)等边三角形.
【解析】
（1）由题意得出△＝0，得出c2＋a2＝b2，由勾股定理的逆定理得出△ABC是直角三角形即可；
（2）由x＝
时函数有最大值
，可知顶点的横坐标为，纵坐标为，根据顶点坐标公式列方程求解即可．
解：(1) 令y＝0，即－(a＋b)x2－2cx＋a－b＝0，
∵抛物线与x轴只有一个交点，
∴△＝4c2－4[－(a＋b)(a－b)]＝0，
化简得：a2＋c2=b2，
∴△ABC是以b为斜边的直角三角形；
(2) 依题意得：x＝
，
∴
，
又
，
∴a2＋2c2－2b2－ab＝0，
将代入a2＋2c2－2b2－ab＝0中，得a2＝b2，
∵a＞0，b＞0，
∴a＝b＝c，
∴△ABC为等边三角形.
练习册系列答案
阅读快车系列答案
相关题目
【题目】遵义市举行中学生“汉字听写大赛”，某校100名学生参加学校选拔赛根据成绩按
、
、
、
四个等级进行统计，绘制了如下不完整的频数分布表和扇形图根据图表中的信息，解答下列问题：
成绩等级频数分布表
成绩等级 | 频数（人数） | 频率 |
| 5 | |
|
| 0.6 |
|
| |
| ||
合计 | 100 | 1 |
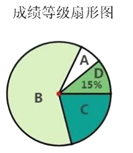
（1）频数分布表中
______，
______；
（2）在扇形图中，求成绩等级“”所对应的圆心角度数；
（3）已知成绩等级“”的5名同学中有3名男同学和2名女同学，现从中挑选2名同学进行答辩培训，请用树状图或列表法列举所有可能，并求挑选出的2名同学恰好是“1男1女”的概率.
