Question

【题目】在平面直角坐标系中，对于半径为的和点，给出如下定义：

若，则称为的“近外点”.

（1）当的半径为2时，点，，，中，的“近外点”是__________；

（2）若点是的“近外点”，求的半径的取值范围；

（3）当的半径为2时，直线与轴交于点，与轴交于点，若线段上存在的“近外点”，直接写出的取值范围.

Answer 1

【答案】（1）B,C; （2）;（3）或.

【解析】

（1）先求出r=3，再分别求出OA，OB，OC，OD，再判断即可求解；
（2）先求出OE，用圆的“近外点”满足的条件建立不等式组求解即可；
（3）先判断出直线MN中OM＞ON，进而得出点M和点G是圆O的“近外点”的分界点，再分两种情况讨论计算即可．

解：（1）∵⊙O的半径为2，
∴r=3，
∵A（4，0），
∴OA=4＞3，
∴点A不是⊙O的“近外点”，
B （-，0），
∴OB=，而2＜＜3，
∴B是⊙O的“近外点”，
C（0，3），
∴OC=3，
∴点C是⊙O的“近外点”，
D （1，-1），
∴OD= = ＜2，
∴点D不是⊙O的“近外点”，
故答案为：B，C；
（2）∵E（3，4），
∴OE= =5，
∵点E是⊙O的“近外点”，
∴，
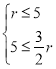∴ ≤r≤5；

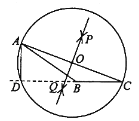
（3）如图，

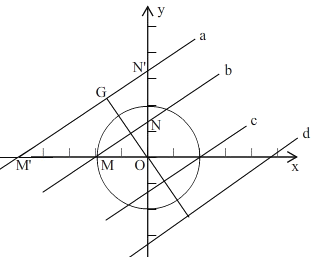
∵直线MN的解析式为，
∴OM＞ON，
①点N在y轴正半轴时，
当点M是⊙O的“近外点”，此时，点M（-2，0），
将M（-2，0）代入直线MN的解析式中，解得，b=，
即：b的最小值为，
过点O作OG⊥M'N'于G，
当点G是⊙O的“近外点”时，此时OG=3，
在Rt△ON'G中，∠ON'G=60°，
∴ON'==2，
b的最大值为2，
∴≤b≤2，
②当点N在y轴负半轴时，同①的方法得出，-2≤b≤-，
即：≤b≤2或-2≤b≤-．