题目内容
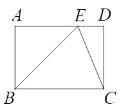
如图,在矩形ABCD中,点E在AD上,且EC平分∠BED.
(1)△BEC是否为等腰三角形?证明你的结论.
(2)已知AB=1,∠ABE=45°,求BC的长.
【答案】(1)见解析;(2) .
.
【解析】(1)由矩形的性质和角平分线的定义得出∠DEC=∠ECB=∠BEC,推出BE=BC即可;
(2)求出AE=AB=1,根据勾股定理求出BE即可.
详解:(1) △BEC为等腰三角形
∵矩形ABCD,∴AD∥BC,
∴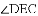
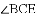
又∵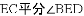
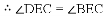

∴△BEC为等腰三角形.
(2)∵矩形ABCD,
∴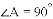 .
.
又∵AB=1,∠ABE=45°∴由勾股定理得
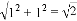 ,
,
由(1)得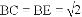 .
.
点睛:本题考查了矩形的性质,等腰三角形的判定,勾股定理的应用,主要考察学生的推理能力,题目比较好,难度适中.
【题型】解答题
【结束】
23
某市为了构建城市立体道路网络,决定修建一条轻轨铁路,为使工程提前半年完成,需要将工作效率提高25%,原计划完成这项工程需要多少个月?
练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目


 sin60°+(π--4)0
sin60°+(π--4)0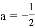 ,b=2.
,b=2.
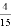 B.
B.  C.
C.  D.
D. 

 ,
, ,
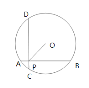
, 均在
均在 的正方形网格格点上,过
的正方形网格格点上,过 ,
, ,
, 三点的外接圆除经过
三点的外接圆除经过 ,
, ,
, 三点外还能经过的格点数为 .
三点外还能经过的格点数为 .
 D.
D.