ƒøƒ⁄»ð
°æƒø°ø∂‘”⁄a°¢b∂®“¡Ω÷÷–¬‘ÀÀ„°∞*°±∫Õ°∞®í°±£∫a*b=a+kb£¨a®íb=ka+b£®∆‰÷–kŒ™≥£ ˝£¨«“k°Ÿ0£©£Æ»Ù∆Ω√Ê÷±Ω«◊¯±ÍœµxOy÷–µƒµ„P£®a£¨b£©£¨”–µ„Pµƒ◊¯±ÍŒ™£®a*b£¨a®íb£©”Î÷Æœý∂‘”¶£¨‘Ú≥∆µ„PŒ™µ„Pµƒ°∞k—Ð…˙µ„°±
¿˝»Á£∫P£®1£¨4£©µƒ°∞2—Ð…˙µ„°±Œ™P°‰£®l+2°¡4£¨2°¡1+4£©£¨º¥P°‰£®9£¨6£©£Æ
£®1£©µ„P£®©Å1£¨6£©µƒ°∞2—Ð…˙µ„°±P°‰µƒ◊¯±ÍŒ™°° °°£Æ
£®2£©»Ùµ„Pµƒ°∞3—Ð…˙µ„°±P°‰µƒ◊¯±ÍŒ™£®5£¨7£©£¨«Ûµ„Pµƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©£®11£¨4£©£ª£®2£©£®2£¨1£©£Æ
°æΩ‚Œˆ°ø
£®1£©÷±Ω”¿˚”√–¬∂®“ÂΩ¯∂¯∑÷Œˆµ√≥ˆ¥∞∏£ª
£®2£©÷±Ω”¿˚”√–¬∂®“ÂΩ·∫œ∂˛‘™“ª¥Œ∑Ω≥Ã◊ȵƒΩ‚∑®µ√≥ˆ¥∞∏£Æ
£®1£©”…“‚ø…µ√£¨µ„P£®©Å1£¨6£©µƒ°∞2—Ð…˙µ„°±P°‰µƒ◊¯±ÍŒ™£∫[©Å1+2°¡6£¨2°¡£®©Å1£©+6]£¨º¥£®11£¨4£©£ª
π ¥∞∏Œ™£∫£®11£¨4£©£ª
£®2£©…˵„Pµƒ◊¯±ÍŒ™£∫£®a£¨b£©£¨
”…“‚ø…µ√£∫![]() £¨
£¨
Ω‚µ√£∫![]() £¨
£¨
°ýµ„Pµƒ◊¯±ÍŒ™£∫£®2£¨1£©£Æ

 ø⁄À„Âø®º””¶”√ºؗµœµ¡–¥∞∏
ø⁄À„Âø®º””¶”√ºؗµœµ¡–¥∞∏ ◊€∫œ◊‘≤‚œµ¡–¥∞∏
◊€∫œ◊‘≤‚œµ¡–¥∞∏°æƒø°øƒ≥÷–—ß柖–°∞–£‘∞∫√…˘“Ù°±∏Ë ÷¥Û»¸£¨≥ı°¢∏þ÷–≤ø∏˘æð≥ı»¸≥…º®£¨∏˜—°≥ˆ![]() √˚—° ÷◊È≥…≥ı÷–¥˙±Ì∂”∫Õ∏þ÷–¥˙±Ì∂”≤Œº”—ß–£æˆ»¸£Æ√ø∏ˆ∂”
√˚—° ÷◊È≥…≥ı÷–¥˙±Ì∂”∫Õ∏þ÷–¥˙±Ì∂”≤Œº”—ß–£æˆ»¸£Æ√ø∏ˆ∂”![]() √˚—° ÷µƒæˆ»¸≥…º®»ÁÕºÀ˘ æ£∫
√˚—° ÷µƒæˆ»¸≥…º®»ÁÕºÀ˘ æ£∫

![]() Ãӱ̣∫
Ãӱ̣∫
∆Ωæ˘ ˝£®∑÷£© | ÷–Œª ˝£®∑÷£© | ÷⁄ ˝£®∑÷£© | |
≥ı÷–¥˙±Ì∂” |
|
| |
∏þ÷–¥˙±Ì∂” |
|
|
![]() Ω·∫œ¡Ω∂”戻¸≥…º®µƒ∆Ωæ˘ ˝∫Õ÷–Œª ˝£¨∑÷Œˆƒƒ∏ˆ¥˙±Ì∂”µƒ≥…º®Ωœ∫√£ª
Ω·∫œ¡Ω∂”戻¸≥…º®µƒ∆Ωæ˘ ˝∫Õ÷–Œª ˝£¨∑÷Œˆƒƒ∏ˆ¥˙±Ì∂”µƒ≥…º®Ωœ∫√£ª
![]() º∆À„¡Ω∂”戻¸≥…º®µƒ∑Ω≤Ó£¨≤¢≈–∂œƒƒ∏ˆ¥˙±Ì∂”µƒ≥…º®ΩœŒ™Œ»∂®£Æ
º∆À„¡Ω∂”戻¸≥…º®µƒ∑Ω≤Ó£¨≤¢≈–∂œƒƒ∏ˆ¥˙±Ì∂”µƒ≥…º®ΩœŒ™Œ»∂®£Æ
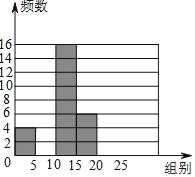
°æƒø°ø÷È∫£ –ƒ≥÷–—ßø™’π÷˜Ã‚Œ™°∞Œ“∞Æ‘ƒ∂¡°±µƒ◊®Ã‚µ˜≤ȪÓ∂Ø£¨Œ™¡ÀΩ‚—ß–£1200√˚—ß…˙“ªƒÍƒ⁄‘ƒ∂¡ Ⱥơø£¨Àʪ˙≥È»°≤ø∑÷—ß…˙Ω¯––Õ≥º∆£¨ªÊ÷∆≥…»Áœ¬…–Œ¥ÕÍ≥…µƒ∆µ ˝∑÷≤º±Ì∫Õ∆µ ˝∑÷≤º÷±∑ΩÕº£Æ«Î∏˘æðÕº±Ì£¨Ω‚¥œ¬√ʵƒŒ £∫
∑÷◊È | ∆µ ˝ | ∆µ¬ |
0°Ðx£º5 | 4 | 0.08 |
5°Ðx£º10 | 14 | 0.28 |
10°Ðx£º15 | 16 | a |
15°Ðx£º20 | b | c |
20°Ðx£º25 | 10 | 0.2 |
∫œº∆ | d | 1.00 |
£®1£©a=°° °°£¨b=°° °°c=°° °°£Æ
£®2£©≤π»´∆µ ˝∑÷≤º÷±∑ΩÕº£ª
£®3£©∏˘æð∏√—˘±æ£¨π¿º∆∏√–£—ß…˙‘ƒ∂¡ 鼮 ˝¡ø‘⁄15±æªÚ15±æ“‘…œµƒ»À ˝£Æ
°æƒø°ø∏∏«◊∏ÊÀþ–°√˜£∫°∞æý¿Îµÿ√Ê‘Ω∏þ£¨Œ¬∂»‘ΩµÕ°±£¨≤¢∏¯–°√˜≥ˆ æ¡Àœ¬√ʵƒ±Ì∏Ò£∫
æý¿Îµÿ√Ê∏þ∂»£®«ß√◊£©h | 0 | 1 | 2 | 3 | 4 | 5 |
Œ¬∂»£®°Ê£©t | 20 | 14 | 8 | 2 | ©Å4 | ©Å10 |
∏˘æð±Ì÷–£¨∏∏«◊ªπ∏¯–°√˜≥ˆ¡Àœ¬√ʺ∏∏ˆŒ £¨«Îƒ„∞Ô÷˙–°√˜ªÿ¥œ¬¡–Œ Â:
£®1£©±Ì÷–◊‘±‰¡ø «°° °°£ª“Ú±‰¡ø «°° °°£ªµ±µÿ√Ê…œ£®º¥h=0 ±£© ±£¨Œ¬∂» «°° °°°Ê£Æ
£®2£©»Áπ˚”√h±Ì ææý¿Îµÿ√ʵƒ∏þ∂»£¨”√t±Ì 挬∂»£¨«Î–¥≥ˆ¬˙◊„t”Îhπÿœµµƒ Ω◊”£Æ
£®3£©º∆À„≥ˆæý¿Îµÿ√Ê6«ß√◊µƒ∏þø’Œ¬∂» «∂ý…Ÿ£ø