题目内容
【题目】如图,![]() 是直线
是直线![]() 上一点,
上一点,![]() 为任一条射线,
为任一条射线,![]() 平分
平分![]() ,
,![]() 平分
平分![]() .
.

(1)找出图中![]() 的补角,
的补角,![]() 的补角;
的补角;
(2)若![]() ,求
,求![]() 和
和![]() 的度数;
的度数;
(3)![]() 与
与![]() 具有怎样的数量关系?说明理由.
具有怎样的数量关系?说明理由.
【答案】(1)![]() 的补角
的补角![]() 或
或![]() ;
;![]() 的补角
的补角![]() 或
或![]() ;(2)
;(2)![]() ,
,![]() ;(3)
;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)根据互为补角的和等于180°找出即可;
(2)根据角平分线的定义求出∠COD的度数即可,先求出∠AOC的度数,再根据角平分线的定义解答;
(3)根据角平分线的定义表示出∠COD与∠EOC,然后整理即可得解.
(1)∵OD平分∠BOC,
∴∠COD=∠BOD.
∵∠AOD+∠BOD=180°,
∴∠AOD的补角为∠BOD,∠COD.
同理:∠BOE的补角为∠AOE,∠COE;
(2)∵OD平分∠BOC,∠BOC=68°,
∴∠COD![]() ∠BOC
∠BOC![]() 68°=34°.
68°=34°.
∵∠BOC=68°,
∴∠AOC=180°﹣∠BOC=180°﹣68°=112°.
∵OE平分∠AOC,
∴∠EOC![]() ∠AOC
∠AOC![]() 112°=56°;
112°=56°;
(3)∵OD平分∠BOC,OE平分∠AOC,
∴∠COD![]() ∠BOC,∠EOC
∠BOC,∠EOC![]() ∠AOC,
∠AOC,
∴∠COD+∠EOC![]() (∠BOC+∠AOC)
(∠BOC+∠AOC)![]() 180°=90°,
180°=90°,
即∠COD+∠EOC=90°.

练习册系列答案
 百年学典课时学练测系列答案
百年学典课时学练测系列答案 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案
相关题目
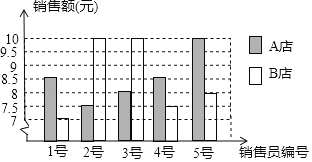
【题目】A、B两店分另选5名销售员某月的销售额(单位:万元)进行分析,数据如下图表(不完整):
平均数 | 中位数 | 众数 | |
A店 | 8.5 |
|
|
B店 |
| 8 | 10 |
(1)根据图a数据填充表格b所缺的数据;
(2)如果A店想让一半以上的销售员达到销售目标,你认为月销售额定为多少合适?说明理由.