МвДҝДЪИЭ
ЎҫМвДҝЎҝИзНј1Ј¬өгOОӘЦұПЯABЙПТ»өгЈ¬№эOөгЧчЙдПЯOCЈ¬К№ЎПAOC:ЎПBOC=1:2Ј¬Ҫ«Т»ЦұҪЗИэҪЗ°еөДЦұҪЗ¶Ҙөг·ЕФЪөгOҙҰЈ¬Т»ұЯOMФЪЙдПЯOBЙПЈ¬БнТ»ұЯONФЪЦұПЯөДПВ·Ҫ.

ЈЁ1Ј©Ҫ«Нј1ЦРөДИэҪЗ°еИЖөгO°ҙДжКұХл·ҪПтРэЧӘЦБНј2өДО»ЦГЈ¬К№өГONВдФЪЙдПЯOBЙПЈ¬ҙЛКұИэҪЗ°еРэЧӘөДҪЗ¶ИОӘ____________¶ИЈ»
ЈЁ2Ј©ФЪЙПКцЦұҪЗИэҪЗ°еҙУНј1ДжКұХлРэЧӘөҪНј3өДО»ЦГөД№эіМЦРЈ¬ИфИэҪЗ°еИЖөгO°ҙ15ЎгГҝГлөДЛЩ¶ИРэЧӘЈ¬өұЦұҪЗИэҪЗ°еөДЦұҪЗұЯONЛщФЪЦұПЯЗЎәГЖҪ·ЦЎПAOCКұЈ¬ЗуҙЛКұИэҪЗ°еИЖөгOөДФЛ¶ҜКұјдtөДЦө.
ЈЁ3Ј©Ҫ«Нј1ЦРөДИэҪЗ°еИЖөгO°ҙГҝГл10ЎгөДЛЩ¶ИСШДжКұХл·ҪПтРэЧӘТ»ЦЬ.ФЪРэЧӘөД№эіМЦРЈ¬јЩИзөЪtГлКұЈ¬OAЎўOCЎўONИэМхЙдПЯ№№іЙПаөИөДҪЗЈ¬ЗуҙЛКұtөДЦөОӘ¶аЙЩЈҝЈЁЦұҪУРҙіцҙр°ёЈ©
Ўҫҙр°ёЎҝЈЁ1Ј©90Ј»ЈЁ2Ј©4»т16ГлЈ»ЈЁ3Ј©tөДЦөОӘ6Ўў15Ўў24Ўў33.
ЎҫҪвОцЎҝКФМв·ЦОцЈәЈЁ1Ј©УЙЎПMON=90ЎгјҙҝЙөГіцҪбВЫЈ»
ЈЁ2Ј©·ЦБҪЦЦЗйҝцМЦВЫјҙҝЙЈ»
ЈЁ3Ј©·ЦЛДЦЦЗйҝцМЦВЫјҙҝЙЈ®
КФМвҪвОцЈәҪвЈәЈЁ1Ј©90Ј»
ЈЁ2Ј©ЈЁiЈ©ИзНјЈ¬

өұЦұҪЗұЯONФЪЎПAOCНвІҝКұЈ¬УЙЦұПЯONЖҪ·ЦЎПAOCЈ¬ҝЙөГЎПBON=30ЎгЈ®ТтҙЛИэҪЗ°еИЖөгOДжКұХлРэЧӘ60ЎгЈ®ҙЛКұИэҪЗ°еөДФЛ¶ҜКұјдОӘЈәt=60ЎгЎВ15Ўг=4ЈЁГлЈ©Ј®
ЈЁўўЈ©ИзНјЈ¬өұЦұҪЗұЯONФЪЎПAOCДЪІҝКұЈ¬УЙЦұПЯONЖҪ·ЦЎПAOCЈ¬ҝЙөГЎПCON=30ЎгЈ®
ТтҙЛИэҪЗ°еИЖөгOДжКұХлРэЧӘ240ЎгЈ®ҙЛКұИэҪЗ°еөДФЛ¶ҜКұјдОӘЈәt=240ЎгЎВ15Ўг=16ЈЁГлЈ©Ј®
ЎаөұИэҪЗ°еИЖөгOФЛ¶ҜБЛ4Гл»т16ГлКұЈ¬ЦұҪЗИэҪЗ°еөДЦұҪЗұЯONЛщФЪЦұПЯЗЎәГЖҪ·ЦЎПAOCЈ®

ЈЁ3Ј©ЎЯЎПAOCЈәЎПBOC=1Јә2Ј¬ЎаЎПAOC=60ЎгЈ¬ЎПBOC=120ЎгЈ®
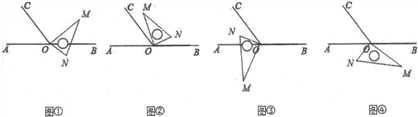
ўЩИзНјўЩЈ¬өұЎПAON=ЎПNOCКұЈ¬ҙЛКұЎПAON=(360ЎгЈӯ60Ўг)ЎВ2=150ЎгЈ¬t=(150ЎгЈӯ90Ўг)ЎВ10Ўг=6ЈЁГлЈ©Ј»
ўЪИзНјўЪЈ¬өұЎПNOC=60ЎгКұЈ¬ҙЛКұРэЧӘөД¶ИКэОӘЈә90Ўг+60Ўг=150ЎгЈ¬t=150ЎгЎВ10Ўг=15ЈЁГлЈ©Ј»
ўЫИзНјўЫЈ¬өұONЖҪ·ЦЎПAOCКұЈ¬ҙЛКұt=(90Ўг+120Ўг+30Ўг)ЎВ10=24ЈЁГлЈ©
ўЬИзНјўЬЈ¬өұЎПAON=ЎПAOCКұЈ¬ҙЛКұt=(90Ўг+180Ўг+60Ўг)ЎВ10=33ЈЁГлЈ©
№КtөДЦөОӘ6Ўў15Ўў24Ўў33Ј®

 ГыРЈҝОМГПөБРҙр°ё
ГыРЈҝОМГПөБРҙр°ё