题目内容
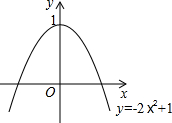 二次函数y=-2x2+1的图象如图所示,将其绕坐标原点O旋转180°,则旋转后的抛物线的解析式为( )
二次函数y=-2x2+1的图象如图所示,将其绕坐标原点O旋转180°,则旋转后的抛物线的解析式为( )| A、y=-2x2-1 |
| B、y=2x2+1 |
| C、y=2x2 |
| D、y=2x2-1 |
考点:二次函数图象与几何变换
专题:
分析:根据原抛物线的顶点坐标求出旋转后的抛物线的顶点坐标,然后根据顶点式解析式形式写出即可.
解答:解:∵二次函数y=-2x2+1的顶点坐标为(0,1),
∴绕坐标原点O旋转180°后的抛物线的顶点坐标为(0,-1),
又∵旋转后抛物线的开口方向上,
∴旋转后的抛物线的解析式为y=2x2-1.
故选D.
∴绕坐标原点O旋转180°后的抛物线的顶点坐标为(0,-1),
又∵旋转后抛物线的开口方向上,
∴旋转后的抛物线的解析式为y=2x2-1.
故选D.
点评:本题考查了二次函数图象与几何变换,此类题目,利用顶点的变化确定抛物线解析式更简便.

练习册系列答案
 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案
相关题目
如果关于x的方程-2x+a=1与
=x+4的解是x=-3,那么字母a的值是( )
| 3x+4 |
| a |
| A、-5 | B、5 | C、0 | D、-5或1 |
 已知图中的两个三角形全等,则∠1等于( )
已知图中的两个三角形全等,则∠1等于( )| A、72° | B、60° |
| C、50° | D、58° |
下列计算正确的是( )
A、9÷2×
| ||||||
B、6÷(
| ||||||
C、
| ||||||
D、-
|
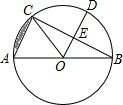 如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6
如图,AB是⊙O的直径,BC是⊙O的弦,半径OD⊥BC,垂足为E,若BC=6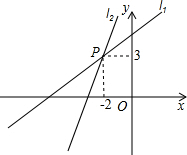 如图,一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P,则方程组
如图,一次函数y=kx1+b1的图象l1与y=kx2+b2的图象l2相交于点P,则方程组