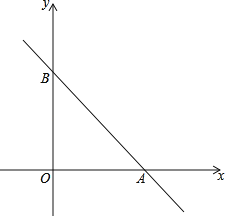题目内容
【题目】如图,直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 、
、![]() 两点.
两点.
(1)求抛物线的解析式;
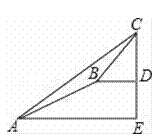
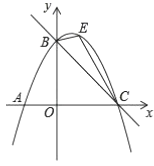
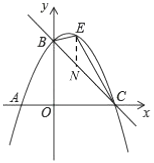
(2)如图,点![]() 是抛物线上的一动点(不与
是抛物线上的一动点(不与![]() ,
,![]() 两点重合),当
两点重合),当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
(3)若点![]() 是抛物线上的一动点,当
是抛物线上的一动点,当![]() 为什么取值范围时,对应的点
为什么取值范围时,对应的点![]() 有且只有两个?
有且只有两个?
【答案】(1)![]() ;(2)
;(2)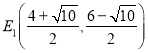 ,
,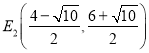 ,
, ,
,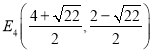 ;(3)当
;(3)当![]() 时,对应的点
时,对应的点![]() 有且只有两个.
有且只有两个.
【解析】
(1)根据待定系数法,即可求解;
(2)过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,设点
,设点![]() ,点
,点![]() ,根据
,根据![]() ,
,![]() ,列出方程,即可求解;
,列出方程,即可求解;
(3)当![]() 点在直线
点在直线![]() 的下方的抛物线上时,一定有两个对应的
的下方的抛物线上时,一定有两个对应的![]() 点满足
点满足![]() 面积为
面积为![]() ,当
,当![]() 点在直线
点在直线![]() 的上方的抛物线上时,无
的上方的抛物线上时,无![]() 点满足
点满足![]() 面积为
面积为![]() 才符合题意,故只需要求出当点
才符合题意,故只需要求出当点![]() 在直线
在直线![]() 的上方时,
的上方时,![]() 的最大值,即可得到结论 .
的最大值,即可得到结论 .
(1)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,
∴![]() ,
,![]() ,
,
将![]() ,
,![]() 代入
代入![]() ,
,
可得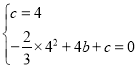 ,解得
,解得![]() ,
,
∴![]() ;
;
(2)如图,过点![]() 作
作![]() 轴的垂线交
轴的垂线交![]() 于点
于点![]() ,
,
设点![]() ,则点
,则点![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,解得:
,解得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
将![]() ,
,![]() ,
,![]() ,
,![]() 代入抛物线解析式,可得:
代入抛物线解析式,可得:![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴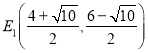 ,
,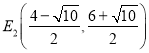 ,
, ,
,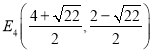 ;
;
(3)当点F在直线BC上方的抛物线上时,设点![]() ,
,
由(2)同理可得:![]() ,
,
∴当![]() 时,
时,![]() 的最大值为
的最大值为![]() ,
,
∴当![]() >
>![]() 时,在直线BC的上方的抛物线上无法找到
时,在直线BC的上方的抛物线上无法找到![]() 点,
点,
综上所述:当![]() 时,对应的点
时,对应的点![]() 有且只有两个.
有且只有两个.

练习册系列答案
 名师伴你成长课时同步学练测系列答案
名师伴你成长课时同步学练测系列答案
相关题目