题目内容
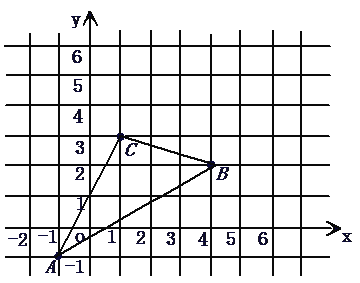
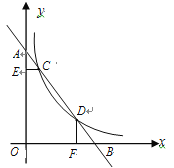
【题目】在平面直角坐标系中,直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于点
轴分别交于点![]() 、点
、点![]() ,与双曲线
,与双曲线![]()
![]() 交于
交于![]() 、
、![]() 两点,
两点,![]() 轴于点
轴于点![]() ,
,![]() 轴于点
轴于点![]() .
.
(1)填空:![]() = ,
= ,![]() = ;
= ;
(2)求直线![]() 的解析式;
的解析式;
(3)求证:![]() .
.
【答案】(1)填空:![]() =6,
=6,![]() =2;
=2;
(2)直线![]() 的解析式为y=-2x+8;
的解析式为y=-2x+8;
(3)证明见解析.
【解析】试题分析:(1)根据反比例函数中k=xy的特点求出k及n的值即可;
(2)设直线AB的解析式为y=kx+b(k≠0),再把A、B两点的坐标代入即可求出k、b的值,进而可求出直线AB的解析式;
(3)在直线y=-2x+8中,令x=0,求出y的值,再令y=0,求出x的值即可得出A、B两点的坐标,CE⊥y轴,DF⊥x轴,故∠AEC=∠DFB=90°,由全等三角形的判定定理即可得出△AEC≌△DFB,由全等三角形的性质即可得出结论.
试题解析:(1)∵点C(1,6)在反比例函数y=![]() 上,
上,
∴m=1×6=6;
∵C(1,6)、D(3,n)两点均在反比例函数y=![]() 上,
上,
∴1×6=3n,解得n=2.
(2)设直线AB的解析式为:![]()
∵直线AB过点(1,6)、D(3,2)两点
∴![]() ,解得
,解得![]()
∴直线AB的解析式为![]() ;
;
(3)在直线![]() 中,令
中,令![]() ,则
,则![]() ,令
,令![]() ,则
,则![]()
∴A(0,8),B(4,0)
∵![]() ,
,![]()
∴![]()
∵![]() ,
,![]()
∴![]()
∴![]()

【题目】某中学举行“感恩资助,立志成才”演讲比赛,根据初赛成绩在七,八年级分别选出10名同学参加决赛,这些选手的决赛成绩如图所示:
根据图和下表提供的信息,解答下列问题:
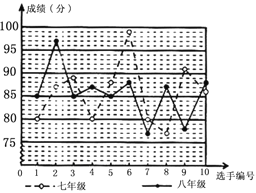
(1)请你把下边的表格填写完整;
成绩统计 | 众数 | 平均数 | 方差 |
七年级 | 85.7 | 39.61 | |
八年级 | 85.7 | 27.81 |
(2)考虑平均数与方差,你认为哪年级的团体成绩更好些;
(3)假设在每个年级的决赛选手中分别选出3人参加总决赛,你认为哪个年级的实力更强一些,请说明理由.
【题目】某商场投入13 800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
类别/单价 | 成本价 | 销售价(元/箱) |
甲 | 24 | 36 |
乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
【题目】商场某柜台销售每台进价分别为160元、120元的A、B两种型号的电风扇,下表是近两周的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一周 | 3台 | 4台 | 1200元 |
第二周 | 5台 | 6台 | 1900元 |
(进价、售价均保持不变,利润=销售收入﹣进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若商场准备用不多于7500元的金额再采购这两种型号的电风扇共50台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,商场销售完这50台电风扇能否实现利润超过1850元的目标?若能,请给出相应的采购方案;若不能,请说明理由.