题目内容
如图1,Rt△ABC中,∠ACB=90°,AC=3,BC=4,点O是斜边AB上一动点,以OA为半径作⊙O与AC边交于点P,

1.当OA=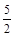 时,求点O到BC的距离
时,求点O到BC的距离
2.如图2,当OA=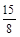 时,求证:直线BC与⊙O相切;此时线段AP的长是多少?
时,求证:直线BC与⊙O相切;此时线段AP的长是多少?
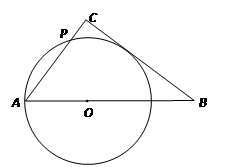
3.若BC边与⊙O有公共点,直接写出 OA
的取值范围;
4.若CO平分∠ACB,则线段AP的长是多少?
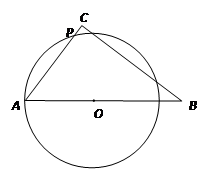
1.解:在Rt△ABE中,![]() . …………… 1分
. …………… 1分
过点O作OD⊥BC于点D,则OD∥AC,
∴△ODB∽△ACB, ∴![]() , ∴
, ∴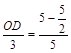 , ∴
, ∴![]() ,
,
∴点O到BC的距离为![]() . ………………………………………………… 3分
. ………………………………………………… 3分
2.证明:过点O作OE⊥BC于点E, OF⊥AC于点F,
∵△OEB∽△ACB, ∴![]() ∴
∴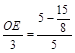 , ∴
, ∴![]() .
.
∴直线BC与⊙O相切. ………………………………………………… 5分
此时,四边形OECF为矩形,
∴AF=AC-FC=3-![]() =
=![]() ,
,
∵OF⊥AC,
∴AP=2AF=![]() . ………………………………………………… 7分
. ………………………………………………… 7分
3.![]() ; ………………………………………………… 9分
; ………………………………………………… 9分
4.点O作OG⊥AC于点G, OH⊥BC于点H,
则四边形OGCH是矩形,且AP=2AG,
又∵CO平分∠ACB,∴OG=OH,∴矩形OGCH是正方形. ………………… 10分
设正方形OGCH的边长为x,则AG=3-x,
∵OG∥BC,
∵△AOG∽△ABC, ∴![]() , ∴
, ∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴AP=2AG=![]() . ………………………………………………… 12分
. ………………………………………………… 12分
解析:略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论:
(2012•和平区二模)如图,在Rt△ABC中,∠BAC=90°,AB=6,AM为∠BAC的平分线,CM=2BM.下列结论: (2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为
(2013•遵义)如图,在Rt△ABC中,∠ACB=90°,AC=BC=1,E为BC边上的一点,以A为圆心,AE为半径的圆弧交AB于点D,交AC的延长于点F,若图中两个阴影部分的面积相等,则AF的长为 如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9cm,则AB的长为( )
如图,在Rt△ABC中,∠C=90°,∠A=30°,AB+BC=9cm,则AB的长为( ) 的外接圆.
的外接圆. (2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.
(2013•嘉定区二模)如图,在Rt△ABC中,∠ACB=90°,点D在AC边上,且BC2=CD•CA.