题目内容
【题目】如图，某船以每小时36海里的速度向正东方向航行，在点A测得某岛C在北偏东60°方向上，航行半小时后到达点B测得该岛在北偏东30°方向上，已知该岛周围16海里内有暗礁．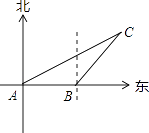
（1）说明点B是否在暗礁区域内；
（2）若继续向东航行有无触礁的危险？请说明理由．
【答案】
（1）
解：作CD⊥AB于点D，
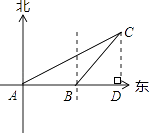
设BC为x，
在Rt△BCD中∠CBD=60°，
∴ 
．
．
在Rt△ACD中∠CAD=30° 
，
∴ 
．
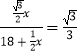∴x=18．
∴B点不在暗礁区域内
（2）
解：∵ 
，
∵ 
，
∴若继续向东航行船有触礁的危险．
【解析】（1）求点B是否在暗礁区域内，其实就是求CB的距离是否大于16，如果大于则不在暗礁区域内，反之则在．可通过构造直角三角形来求CB的长，作CD⊥AB于点D，CD是直角三角形ACD和CBD的公共直角边，可先求出CD的长，再求出CB的长；（2）本题实际上是问，C到AB的距离即CD是否大于16，如果大于则无触礁危险，反之则有，CD的值，（1）已经求出，只要进行比较即可．
【考点精析】关于本题考查的关于方向角问题，需要了解指北或指南方向线与目标方向 线所成的小于90°的水平角，叫做方向角才能得出正确答案．
练习册系列答案
相关题目
